(1)证明:∵AC是半圆O的直径,
∴∠ADC=90°.
∵D是弧AB的中点,
∴

=

,
∴∠ACD=∠BCD.
∵在△ACD与△ECD中,
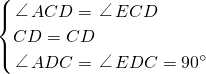
,
∴△ACD≌△ECD(ASA),
∴CA=CE;
(2)解:∵OA=OB,∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=OB,∠OAB=60°.
∵在△CDE与△ABE中,
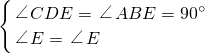
,
∴△CDE∽△ABE,
∴DE:BE=CE:AE,
∴DE•AE=BE•CE,
∵△ACD≌△ECD,
∴AD=DE=

AE,
∵CE=CA=2OA=2AB,
∴

AE•AE=BE•2AB,
∴AE
2=4BE•AB.
设AB=x,BE=y,则4xy=AE
2=24(2-

),
即2xy=12(2-

) ①.
在△ABE中,∵∠ABE=90°,
∴AB
2+BE
2=AE
2,
∴x
2+y
2=24(2-

) ②,
①+②,得x
2+y
2+2xy=36(2-

),
∵x>0,y>0,
∴x+y=3

-3

③,
②-①,得x
2+y
2-2xy=12(2-

),
∵x>y,
∴x-y=3

-

④,
③与④联立,解得
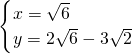
,
∴OA=AB=

,
∴半圆O的面积

π×(

)
2=3π.
分析:(1)由AC是半圆O的直径得到∠ADC=90°,由D是弧AB的中点得到∠ACD=∠BCD,再利用ASA证明△ACD≌△ECD,根据全等三角形的对应边相等即可得到CA=CE;
(2)先根据有一个角为60°的三角形是等边三角形得出△AOB是等边三角形,由等边三角形的性质得到AB=OA=OB,∠OAB=60°,再由两角对应相等的两三角形相似得到△CDE∽△ABE,根据相似三角形对应边成比例得出DE:BE=CE:AE,将DE=

AE,CE=2AB代入,得到AE
2=4BE•AB,又在△ABE中,运用勾股定理得出AB
2+BE
2=AE
2,将
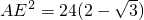
分别代入上面两个式子,求出AB的值,然后根据圆的面积根据即可得出半圆O的面积.
点评:本题考查了圆周角定理,全等三角形、等边三角形、相似三角形的判定与性质,勾股定理,圆的面积及方程思想,综合性较强,有一定难度.

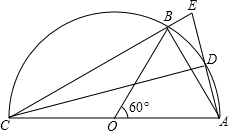
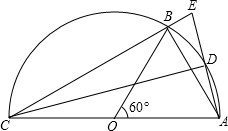 如图,AC是半圆O的直径,B是半圆上的一点,D是弧AB的中点,连接AB、CB、CD、AD,延长AD交CB的延长线于点E.
如图,AC是半圆O的直径,B是半圆上的一点,D是弧AB的中点,连接AB、CB、CD、AD,延长AD交CB的延长线于点E.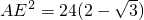 ,求半圆O的面积.
,求半圆O的面积. =
= ,
, ∵在△ACD与△ECD中,
∵在△ACD与△ECD中,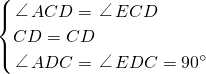 ,
,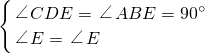 ,
, AE,
AE, AE•AE=BE•2AB,
AE•AE=BE•2AB, ),
), ) ①.
) ①. ) ②,
) ②, ),
), -3
-3 ③,
③, ),
), -
- ④,
④,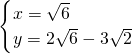 ,
, ,
, π×(
π×( )2=3π.
)2=3π. AE,CE=2AB代入,得到AE2=4BE•AB,又在△ABE中,运用勾股定理得出AB2+BE2=AE2,将
AE,CE=2AB代入,得到AE2=4BE•AB,又在△ABE中,运用勾股定理得出AB2+BE2=AE2,将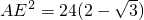 分别代入上面两个式子,求出AB的值,然后根据圆的面积根据即可得出半圆O的面积.
分别代入上面两个式子,求出AB的值,然后根据圆的面积根据即可得出半圆O的面积.

