
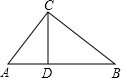
 红星中学计划把一块形状如图所示的废弃荒地开辟为生物园,测得AC=75m,BC=100m,AB=125m.如果沿CD修一条水渠且D点在边AB上,水渠的造价为10元/m,问D点在什么位置时,水渠的造价最低?最低造价是多少?
红星中学计划把一块形状如图所示的废弃荒地开辟为生物园,测得AC=75m,BC=100m,AB=125m.如果沿CD修一条水渠且D点在边AB上,水渠的造价为10元/m,问D点在什么位置时,水渠的造价最低?最低造价是多少? 分析 当CD⊥AB时,水渠的造价最低.由勾股定理的逆定理推知∠ACB=90°,所以结合面积法来求CD的长度,然后求其造价即可.
解答  解:如图,∵AC=75m,BC=100m,AB=125m.
解:如图,∵AC=75m,BC=100m,AB=125m.
∴AC2+BC2=AB2=15625,
∴∠ACB=90°,
当CD⊥AB时,水渠的造价最低.
此时由$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC,
则CD=$\frac{AC•BC}{AB}$=$\frac{75×100}{125}$=60(m),
故60×10=600(元).
答:当CD⊥AB时,水渠的造价最低,最低造价是600元.
点评 本题考查了勾股定理、勾股定理的逆定理.利用勾股定理求几何图形的面积和有关线段的长度.


科目:初中数学 来源: 题型:解答题
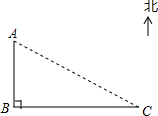 如图,在海上观察所A处.我边防海警发现正南方向60海里的B处有一可疑船只正以每小时20海里的速度向正东方向C处驶去,我边防海警即刻从A处派快艇去拦截.若快艇的速度是每小时$\frac{100}{3}$海里.问快艇最快几小时拦截住可疑船只?
如图,在海上观察所A处.我边防海警发现正南方向60海里的B处有一可疑船只正以每小时20海里的速度向正东方向C处驶去,我边防海警即刻从A处派快艇去拦截.若快艇的速度是每小时$\frac{100}{3}$海里.问快艇最快几小时拦截住可疑船只?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
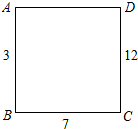 如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的
如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
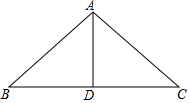 如图,木工师傅做一个“人”字形屋梁,上弦AB=AC=4m,跨度BC为6m.现有一根木料打算做中柱AD (AD是△ABC的中线),请你通过计算求出中柱AD的长度.(只考虑长度,不计损耗)
如图,木工师傅做一个“人”字形屋梁,上弦AB=AC=4m,跨度BC为6m.现有一根木料打算做中柱AD (AD是△ABC的中线),请你通过计算求出中柱AD的长度.(只考虑长度,不计损耗)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
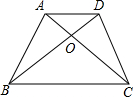 如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果S△ACD:S△ABC=1:2,那么S△AOD:S△BOC是( )
如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果S△ACD:S△ABC=1:2,那么S△AOD:S△BOC是( )| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com