Question

如图，点A（1，1），B（3，1），C（3，-1），D（1，-1）构成正方形ABCD，以AB为边做等边△ABE，则∠ADE和点E的坐标分别为

1. A.
   15°和（2，1+）
2. B.
   75°和（2，-1）
3. C.
   15°和（2，1+）或75°和（2，-1）
4. D.
   15°和（2，1+）或75°和（2，1-）

Answer 1

D
分析：分为两种情况：①当△ABE在正方形ABCD外时，过E作EM⊥AB于M，根据等边三角形性质求出AM、AE，根据勾股定理求出EM，即可得出E的坐标，求出∠EAD，根据三角形的内角和定理和等腰三角形性质即可求出∠ADE；②当等边△ABE在正方形ABCD内时，同法求出此时E的坐标，求出∠DAE，根据三角形的内角和定理和等腰三角形性质即可求出∠ADE．
解答：
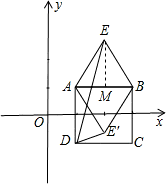
分为两种情况：①△ABE在正方形ABCD外时，如图，过E作EM⊥AB于M，
∵等边三角形ABE，
∴AE=AB=3-1=2，
∴AM=1，
由勾股定理得：AE²=AM²+EM²，
∴2²=1²+EM²，
∴EM=，
∵A（1，1），
∴E的坐标是（2，1+），
∵等边△ABE和正方形ABCD，
∴∠DAB=90°，∠EAB=60°，AD=AE，
∴∠ADE=∠AED=（180°-90°-60°）=15°；
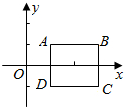
②同理当△ABE在正方形ABCD内时，同法求出E的坐标是（2，-+1），
∵∠DAE=90°-60°=30°，
AD=AE，
∴∠ADE=∠AED=（180°-30°）=75°；
∴∠ADE和点E的坐标分别为15°，（2，1+）或75°，D（2，-+1），
故选D．
点评：本题考查了等边三角形性质、勾股定理、等腰三角形性质、正方形性质、坐标与图形性质、三角形的内角和定理等知识点的运用，主要考查学生综合运用性质进行推理和计算的能力，本题综合性比较强，有一定的难度，但题型较好，注意要分类讨论啊．