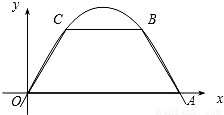
(2011•广东模拟)一开口向上的抛物线与x轴交于A,B两点,C(m,-2)为抛物线顶点,且AC⊥BC.
(1)若m是常数,求抛物线的解析式;
(2)设抛物线交y轴正半轴于D点,抛物线的对称轴交x轴于E点.问是否存在实数m,使得△EOD为等腰三角形?若存在,求出m的值;若不存在,请说明理由.
【答案】
分析:(1)设抛物线的解析式为:y=a(x-m)
2-2,由AC⊥BC,由抛物线的对称性可知:△ACB为等腰直角三角形,可解得B点坐标,进而求出a的值.(2)设存在实数m,使得△EOD为等腰三角形,由(1)知D点坐标,
若△EOD为等腰三角形,只能OD=OE,分类点E在x轴位置情况,求出m的值.
解答:解:(1)设抛物线的解析式为:y=a(x-m)
2-2,
∵AC⊥BC,
∵由抛物线的对称性可知:△ACB为等腰直角三角形,
又∵AB=4,
∴B(m+2,0)
代入y=a(x-m)
2-2,得a=

.
∴解析式为:
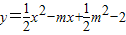
.
(2)由(1)得D(0,

m
2-2),
设存在实数m,使得△EOD为等腰三角形.
∵△EOD为等腰三角形,
∴只能OD=OE.
①当点E在x轴正半轴,
∵m>0时,∴

m
2-2=m.
解得m=
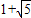
或m=
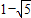
(舍).
②当点E在x轴负半轴,∵m<0时,∴

m
2-2=-m.
解得m=
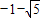
或m=
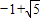
(舍);
③当点E在原点,即m=0时,B、O、D三点共线(不合题意,舍)
综上所述:存在实数m=

或m=

,使得△EOD为等腰三角形.
点评:本题二次函数的综合题,涉及到知识点求解抛物线的解析式,分类讨论思想,此题不是很难,但要仔细.

 .
.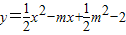 .
. m2-2),
m2-2), m2-2=m.
m2-2=m.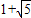 或m=
或m=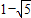 (舍).
(舍). m2-2=-m.
m2-2=-m.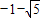 或m=
或m=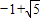 (舍);
(舍); 或m=
或m= ,使得△EOD为等腰三角形.
,使得△EOD为等腰三角形.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案