
 如图,已知△ABC中,AB=AC,∠B=2∠A,DE垂直平分AC交AB于点D,交AC于点E.求证:AD=BC.
如图,已知△ABC中,AB=AC,∠B=2∠A,DE垂直平分AC交AB于点D,交AC于点E.求证:AD=BC.

 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,小明作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积,用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…求第10个正△A10B10C10的面积.
如图,小明作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积,用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…求第10个正△A10B10C10的面积.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,某村有一口呈四边形的池塘,在它的四个角A,B,C,D处各栽有一棵大树.该村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保留四棵大树,并要求扩建后的池成平行四边形,请问:村长能否实现这一设想?若能,请你帮村长设计并画出图形;若不能,请说明理由.
如图,某村有一口呈四边形的池塘,在它的四个角A,B,C,D处各栽有一棵大树.该村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保留四棵大树,并要求扩建后的池成平行四边形,请问:村长能否实现这一设想?若能,请你帮村长设计并画出图形;若不能,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
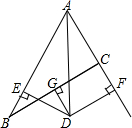 如图所示,在△ABC中,AB=8,AC=4,∠BAC的平分线与BC的垂直平分线交于点D,过点D作DE⊥AB于点E,DF⊥AC(或AC的延长线)于点D.
如图所示,在△ABC中,AB=8,AC=4,∠BAC的平分线与BC的垂直平分线交于点D,过点D作DE⊥AB于点E,DF⊥AC(或AC的延长线)于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,在四边形ABCD中,O是AC和BD的交点,点E,F,G,H分别是AO,BO,CO,DO的中点,如果四边形EFGH是平行四边形,那么四边形ABCD也是平行四边形吗?说说你的理由.
如图所示,在四边形ABCD中,O是AC和BD的交点,点E,F,G,H分别是AO,BO,CO,DO的中点,如果四边形EFGH是平行四边形,那么四边形ABCD也是平行四边形吗?说说你的理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com