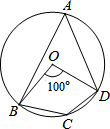
如图.四边形ABCD为⊙O的内接四边形.已知∠BOD=100°.则∠BCD的度数为( )A．50°B．80°C．100°D．130° 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

17．

如图，四边形ABCD为⊙O的内接四边形，已知∠BOD=100°，则∠BCD的度数为（　　）

A．

50°

B．

80°

C．

100°

D．

130°

分析首先根据圆周角与圆心角的关系，求出∠BAD的度数；然后根据圆内接四边形的对角互补，用180°减去∠BAD的度数，求出∠BCD的度数是多少即可．

解答解：∵∠BOD=100°，
∴∠BAD=100°÷2=50°，
∴∠BCD=180°-∠BAD
=180°-50°
=130°
故选：D．

点评（1）此题主要考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半，要熟练掌握．
（2）此题还考查了圆内接四边形的性质，要熟练掌握，解答此题的关键是要明确：①圆内接四边形的对角互补． ②圆内接四边形的任意一个外角等于它的内对角（就是和它相邻的内角的对角）．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

7．运动会上，某班级买了两种矿泉水，其中甲种矿泉水共花费40元，乙种矿泉水共花费30元．甲种矿泉水比乙种矿泉水多买20瓶，且乙种矿泉水的价格是甲种矿泉水价格的1.5倍．若设甲种矿泉水价格为x元/瓶，根据题意可列方程为（　　）

A．

$\frac{40}{1.5x}-\frac{30}{x}$=20

B．

$\frac{40}{x}-\frac{30}{1.5x}$=20

C．

$\frac{30}{x}-\frac{40}{1.5x}$=20

D．

$\frac{30}{1.5x}-\frac{40}{x}$=20

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

8．已知Rt△ABC中，AB是⊙O的弦，斜边AC交⊙O于点D，且AD=DC，延长CB交⊙O于点E．
（1）图1的A、B、C、D、E五个点中，是否存在某两点间的距离等于线段CE的长？请说明理由；
（2）如图2，过点E作⊙O的切线，交AC的延长线于点F．
①若CF=CD时，求sin∠CAB的值；
②若CF=aCD（a＞0）时，试猜想sin∠CAB的值．（用含a的代数式表示，直接写出结果）

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

5．

将正方形ABCD绕点A按逆时针方向旋转30°，得正方形AB₁C₁D₁，B₁C₁交CD于点E，AB=$\sqrt{3}$，则四边形AB₁ED的内切圆半径为（　　）

A．

$\frac{\sqrt{3}+1}{2}$

B．

$\frac{3-\sqrt{3}}{2}$

C．

$\frac{\sqrt{3}+1}{3}$

D．

$\frac{3-\sqrt{3}}{3}$

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

12．下列命题是真命题的是（　　）

	A．	对角线互相平分的四边形是平行四边形
	B．	对角线相等的四边形是矩形
	C．	对角线互相垂直的四边形是菱形
	D．	对角线互相垂直的四边形是正方形

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

2．下列说法正确的是（　　）

	A．	掷一枚均匀的骰子，骰子停止转动后，6点朝上是必然事件
	B．	甲、乙两人在相同条件下各射击10次，他们的成绩平均数相同，方差分别是S_甲²=0.4，S_乙²=0.6，则甲的射击成绩较稳定
	C．	“明天降雨的概率为$\frac{1}{2}$”，表示明天有半天都在降雨
	D．	了解一批电视机的使用寿命，适合用普查的方式