
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
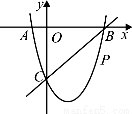
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
(1)二次函数的表达式为:y=x2﹣2x﹣3;(2)P点的坐标为(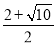 ,
, );(3)P点的坐标为(
);(3)P点的坐标为(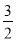 ,
,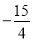 ),四边形ABPC的面积的最大值为
),四边形ABPC的面积的最大值为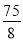 .
.
【解析】
试题分析:(1)将B、C的坐标代入抛物线的解析式中即可求得待定系数的值;
(2)由于菱形的对角线互相垂直平分,若四边形POP′C为菱形,那么P点必在OC的垂直平分线上,据此可求出P点的纵坐标,代入抛物线的解析式中即可求出P点的坐标;
(3)由于△ABC的面积为定值,当四边形ABPC的面积最大时,△BPC的面积最大;过P作y轴的平行线,交直线BC于Q,交x轴于F,易求得直线BC的解析式,可设出P点的横坐标,然后根据抛物线和直线BC的解析式求出Q、P的纵坐标,即可得到PQ的长,以PQ为底,B点横坐标的绝对值为高即可求得△BPC的面积,由此可得到关于四边形ACPB的面积与P点横坐标的函数关系式,根据函数的性质即可求出四边形ABPC的最大面积及对应的P点坐标.
试题解析:(1)将B、C两点的坐标代入得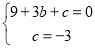 ,
,
解得: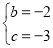 ;
;
所以二次函数的表达式为:y=x2﹣2x﹣3
(2)存在点P,使四边形POP′C为菱形;
设P点坐标为(x,x2﹣2x﹣3),PP′交CO于E
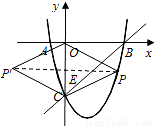
若四边形POP′C是菱形,则有PC=PO;
连接PP′,则PE⊥CO于E,
∴OE=EC=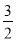
∴y= ;(6分)
;(6分)
∴x2﹣2x﹣3=
解得x1=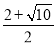 ,x2=
,x2=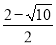 (不合题意,舍去)
(不合题意,舍去)
∴P点的坐标为(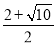 ,
, )(8分)
)(8分)
(3)过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,x2﹣2x﹣3),
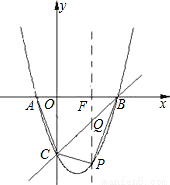
易得,直线BC的解析式为y=x﹣3
则Q点的坐标为(x,x﹣3);
S四边形ABPC=S△ABC+S△BPQ+S△CPQ
=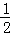 ABOC+
ABOC+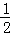 QPBF+
QPBF+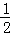 QPOF
QPOF
=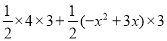
=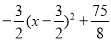
当x=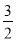 时,四边形ABPC的面积最大
时,四边形ABPC的面积最大
此时P点的坐标为(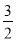 ,
,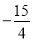 ),四边形ABPC的面积的最大值为
),四边形ABPC的面积的最大值为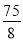 .
.
考点:二次函数综合题.


科目:初中数学 来源:2014-2015学年江苏省九年级上学期期末考试数学试卷(解析版) 题型:选择题
在一副扑克牌(54张,其中王牌两张)中,任意抽取一张牌是“王牌”的概率是
A.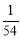 B.
B.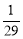 C.
C.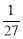 D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省九年级上学期期末考试数学试卷(解析版) 题型:选择题
小明制作了十张卡片,上面分别标有1~10这十个数字.从这十张卡片中随机抽取一张恰好能被4整除的概率是( )
A.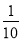 B.
B.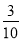 C.
C.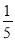 D.
D.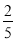
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省尤溪县九年级上学期期末学习效果评价数学试卷(解析版) 题型:解答题
在一个不透明的袋子中装有(除颜色外)完全相同的红色小球1个,白色小球1个和黄色小球2个,
(1)从中先摸出一个小球,记录下它的颜色后,将它放回袋中搅匀,再摸出一个小球,记录下颜色. 求摸出的两个小球的颜色恰好是“一红一黄”的概率是多少?
(2)如果摸出第一个小球之后不放回袋中,再摸出第二个小球,这时摸出的两个小球的颜色恰好是“一红一黄”的概率是多少?
(3)小明想给袋中加入一些红色的小球,使从袋中任意摸出一个小球恰为红色的概率为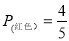 ,请你帮小明算一算,应该加入多少个红色的小球?
,请你帮小明算一算,应该加入多少个红色的小球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com