
(本题满分12分)如图1,抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点.(1)求抛物线的解析式;
(2)设抛物线的顶点为M,直线y=-2x+9与y轴交于点C,与直线OM交于点D.现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)只有一个公共点,求它的顶点横坐标的值或取值范围;
(3)如图2,将抛物线平移,当顶点至原点时,过Q(0,3)作不平行于x轴的直线交抛物线于E,F两点.问在y轴的负半轴上是否存在点P,使△PEF的内心在y轴上.若存在,求出点P的坐标;若不存在,请说明理由.
(1)抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点
∴9a-3b+3=0 且a-b+3=0解得a=1b=4
∴抛物线的解析式为y=x2+4x+3
(2)由(1)配方得y=(x+2)2-1
∴抛物线的顶点M(-2,,1)∴直线OD的解析式为y=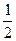 x
x
于是设平移的抛物线的顶点坐标为(h,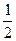 h),
h),
∴平移的抛物线解析式为y=(x-h)2+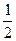 h.
h.
①当抛物线经过点C时,∵C(0,9),∴h2+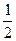 h=9,
h=9,
解得h=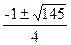 .
.
∴ 当  ≤h<
≤h<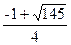 时,平移的抛物线与射线CD只有一个公共点.
时,平移的抛物线与射线CD只有一个公共点.
②当抛物线与直线CD只有一个公共点时,
由方程组y=(x-h)2+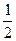 h,y=-2x+9.
h,y=-2x+9.
得 x2+(-2h+2)x+h2+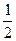 h-9=0,∴△=(-2h+2)2-4(h2+
h-9=0,∴△=(-2h+2)2-4(h2+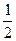 h-9)=0,
h-9)=0,
解得h=4.
此时抛物线y=(x-4)2+2与射线CD唯一的公共点为(3,3),符合题意.
综上:平移的抛物线与射线CD只有一个公共点时,顶点横坐标的值或取值范围是 h=4或  ≤h<
≤h<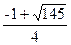 .
.
(3)方法1将抛物线平移,当顶点至原点时,其解析式为y=x2,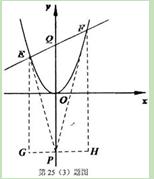
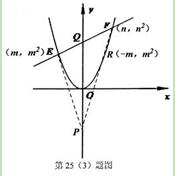
设EF的解析式为y=kx+3(k≠0).
假设存在满足题设条件的点P(0,t),如图,过P作GH∥x轴,分别过E,F作GH的垂线,垂足为G,H.∵△PEF的内心在y轴上,∴∠GEP=∠EPQ=∠QPF=∠HFP,∴△GEP∽△HFP,...............9分∴GP/PH=GE/HF,
∴-xE/xF=(yE-t)/(yF-t)=(kxE+3-t)/(kxF+3-t)
∴2kxE·xF=(t-3)(xE+xF)
由y=x2,y=-kx+3.得x2-kx-3=0.
∴xE+xF=k,xE·xF=-3.∴2k(-3)=(t-3)k,∵k≠0,∴t=-3.∴y轴的负半轴上存在点P(0,-3),使△PEF的内心在y轴上.
方法2 设EF的解析式为y=kx+3(k≠0),点E,F的坐标分别为(m,m2)(n,n2)由方法1知:mn=-3.作点E关于y轴的对称点R(-m,m2),作直线FR交y轴于点P,由对称性知∠EPQ=∠FPQ,∴点P就是所求的点.由F,R的坐标,可得直线FR的解析式为y=(n-m)x+mn.当x=0,y=mn=-3,∴P(0,-3).∴y轴的负半轴上存在点P(0,-3),使△PEF的内心在y轴上.
解析


科目:初中数学 来源: 题型:
(本题满分12分)
如图,直角梯形ABCD中,AB∥DC,![]() ,
,![]() ,
,![]() .动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).

(1)当![]() 时,求线段
时,求线段 的长;
的长;
(2)当0<t<2时,如果以C、P、Q为顶点的三角形为直角三角形,求t的值;
(3)当t>2时,连接PQ交线段AC于点R.请探究![]() 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(贵州铜仁卷)数学 题型:解答题
(本题满分12分)如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.
(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
 |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年上海市徐汇区中考一模数学卷 题型:解答题
(本题满分12分)
如图, 的顶点A、B在二次函数
的顶点A、B在二次函数 的图像上,又点A、B[来分别在
的图像上,又点A、B[来分别在 轴和
轴和 轴上,
轴上, ∠ABO=
∠ABO= .
.

1.(1)求此二次函数的解析式;(4分)
2.
|
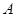 作
作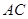 ∥
∥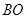 交上述函数图像于点
交上述函数图像于点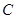 ,
,
点 在上述函数图像上,当
在上述函数图像上,当 与
与 相似时,求点
相似时,求点 的坐标.(8分)
的坐标.(8分)
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生考试数学卷(广东珠海) 题型:解答题
(本题满分12分)如图1,抛物线 与x轴交于A、C两点,与y轴交于B点,与直线
与x轴交于A、C两点,与y轴交于B点,与直线 交于A、D两点。
交于A、D两点。
⑴直接写出A、C两点坐标和直线AD的解析式;
⑵如图2,质地均匀的正四面体骰子的各个面上依次标有数字-1、1、3、4.随机抛掷这枚骰子两次,把第一次着地一面的数字m记做P点的横坐标,第二次着地一面的数字n记做P点的纵坐标.则点 落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?


查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(广西桂林) 题型:解答题
(本题满分12分)
如图,直角梯形ABCD中,AB∥DC, ,
, ,
, .动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).

(1)当 时,求线段
时,求线段 的长;
的长;
(2)当0<t<2时,如果以C、P、Q为顶点的三角形为直角三角形,求t的值;
(3)当t>2时,连接PQ交线段AC于点R.请探究 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com