如图1，在3×3的正方形网格图中，除最中间的格子外，其余每个格子上都有一个数．给出如下的“跳格子”游戏规则：对于任一格子上的数m，若m为正数，则从数m所在的格子开始，按顺时针方向连续跳m个格子，把该格子上的数记为m
1；若m为负数，则从数m所在的格子开始，按逆时针方向连续跳|m|个格子，把该格子上的数记为m
1（上述过程称为跳一次格子）；对于数m
1，继续按上面的游戏规则跳格子，得到数m
2；再继续跳下去，得到m
3，m
4，…，m
n．例如m=2时，如图2所示，从“2”所在的格子开始，按顺时针方向连续跳两个格子，得到m
1=-4；继续跳下去，如图3所示，从“-4”所在的格子开始，按逆时针方向连续跳4个格子，得m
2=-7；…
若a=-2
2+1，b=-2-4，c=（-1）
2011，d=（-3）
2，
①求
a1d1-+c1的值（其中a
1，b
1，c
1，d
1分别表示a，b，c，d按“跳格子”游戏规则跳一次后所得的数）；
②解关于x的方程：
(x-b2)=(x-c2)（其中a
2，b
2，c
2分别表示a，b，c连续跳2次后所得的数，d
3表示d连续跳3次后所得的数）．
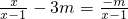，得
等，当m为________时，此根为增根．
轻松课堂单元期中期末专题冲刺100分系列答案
=1，
，得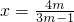
等，当m为（ ）时，此根为增根。