
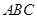 中,∠
中,∠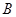 =30°,
=30°,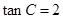 ,
,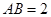 ,求△
,求△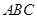 的周长. (结果保留根号)
的周长. (结果保留根号)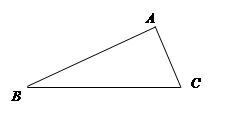
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
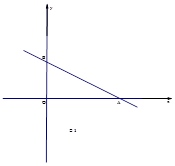
 分别与x轴、y轴交于点A、B,
分别与x轴、y轴交于点A、B,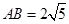 .
.
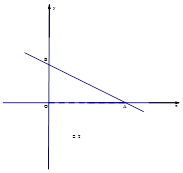
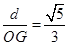 ,若存在,求出t值;若不存在,请说明理由.
,若存在,求出t值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
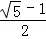 AB;③PB=
AB;③PB=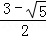 AB;④
AB;④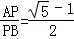 ;⑤
;⑤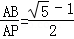 .其中正确的是 (填“序号”)
.其中正确的是 (填“序号”)查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
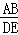 = _____,
= _____,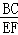 = ____,我们会得到AB与DE这两条线段的比值与BC,EF这两条线段的比值 _____(填相等或不相等),即
= ____,我们会得到AB与DE这两条线段的比值与BC,EF这两条线段的比值 _____(填相等或不相等),即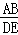 =
=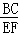 ,那么这四条线段叫做 ______ ,简称比例线段.
,那么这四条线段叫做 ______ ,简称比例线段.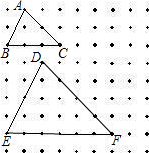
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.1个; | B.2个; | C.3个; | D.4个. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com