
分析 (1)先利用等腰直角三角形得出PM=BM,QN=CN,再利用线段的和差和PM=QN即可得出x;
(2)分三种情况讨论计算,①点P,Q都在AB上,②点P在AB上,点Q在AC上,③点P,Q都在AC上,利用等腰直角三角形的性质和线段的和差即可得出结论.
解答 解:(1)如图1,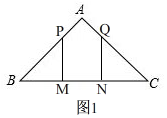 在△ABC中,AB=AC,∠BAC=90°,
在△ABC中,AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵PM⊥BC,QN⊥BC,
∴∠PMB=∠QNC=90°,
在Rt△PMB中,PM=BM,
同理:QN=CN,
∵PM=QN,
∴BM=CN,
∵BC=4,MN=1,
∴BC=BM+MN+CN=2BM+MN=4,
∴BM=$\frac{1}{2}$(4-MN)=$\frac{3}{2}$,
∴x=$\frac{3}{2}$;
(2)①、如图2,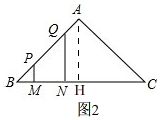 在等腰直角三角形ABC中,BC=4,
在等腰直角三角形ABC中,BC=4,
∴BH=CH=$\frac{1}{2}$BC=2,
∵MN=1,
∴BM<1
当0≤x≤1时,
在Rt△OMB中,∠ABC=45°,
∴PM=BM=x,
在Rt△QNB中,QN=BN=BM+MN=x+1,
∴y=PM+QN=x+x+1=2x+1,
②、如图3,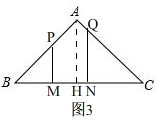 当1<x<2时,同①得,PM=BM=x,
当1<x<2时,同①得,PM=BM=x,
在Rt△QNC中,QN=CN,
∵BC=BM+MN+CN,
∴QN=CN=BC-BM-MN=4-x-1=3-x,
∴y=PM+QN=x+3-x=3;
③、如图4,当2≤x≤3时,
∵BC=4,BM=x,
∴CM=BC-BM=4-x,
∵MN=1,
∴CN=CM-MN=4-x-1=3-x,
在Rt△PMC中,PM=CM=4-x,
同理:QN=CN=3-x,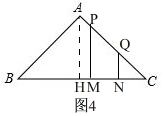
∴y=PM+QN=4-x+3-x=7-2x;
即:y=$\left\{\begin{array}{l}{2x+1(0≤x≤1)}\\{3(1<x<2)}\\{7-2x(2≤x≤3)}\end{array}\right.$.
点评 此题是三角形综合题,主要考查了等腰直角三角形的性质,线段的和差,解本题的关键是用x表示出PM,QN;是一道比较简单的综合题目.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
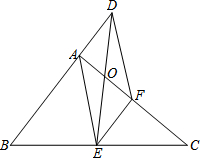 在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使AB=2AD,连接DE、DF、AE、EF,AF与DE交于点O.
在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使AB=2AD,连接DE、DF、AE、EF,AF与DE交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
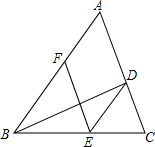 如图,BD是△ABC的角平分线,点E,F分别在边BC,AB上,且DE∥AB,BE=AF.
如图,BD是△ABC的角平分线,点E,F分别在边BC,AB上,且DE∥AB,BE=AF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com