①②③
分析:作出常用辅助线,过圆心连接切点,利用切线的性质定理,可以求出各边以及各角之间的关系.
解答:

解:连接OD,
∵CD是圆的切线
∴OD⊥CD
当AD=CD,∴∠A=∠C
∵AO=OD,∠A=∠ADO,∴∠A=∠C=∠ADO,
又∵∠DOC=∠A+∠ADO
∵∠DOC+∠C=90°
∴∠A=∠C=∠ADO=30°
根据在直角三角形中,30°所对的边是斜边的一半,OD=

OC=R
∵OB=R,所以BC=R
即:①AD=CD符合要求,
当∠A=30°,∵AO=OD
∴∠ADO=30°,
∴∠DOC=60°,
∵OD⊥CD,
∴∠C=30°
根据在直角三角形中,30°所对的边是斜边的一半,OD=

OC=R
∵OB=R,所以BC=R
即:②∠A=30°正确
当∠ADC=120°,OD⊥CD
∴∠ADO=30°,∠A=30°
∴∠DOC=60°
∴∠C=30°
根据在直角三角形中,30°所对的边是斜边的一半,OD=

OC=R
∵OB=R,所以BC=R
即:③∠ADC=120°正确,
当DC=R,∵OD=R,OD⊥CD,
∴OC=

R,∵OB=R,∴BC=

R-R
所以④DC=R,不能使得BC=R
故填:①②③
点评:此题主要考查了切线的性质定理,是中考中常见问题,但是它具有一定的开放性,题目不错.

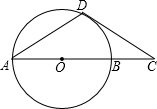 如图,D是半径为R的⊙O上一点,过点D作⊙O的切线交直径AB的延长线于点C,下列四个条件:①AD=CD;②∠A=30°;③∠ADC=120°;④DC=R.其中,使得BC=R的有(填正确结论的序号)________.
如图,D是半径为R的⊙O上一点,过点D作⊙O的切线交直径AB的延长线于点C,下列四个条件:①AD=CD;②∠A=30°;③∠ADC=120°;④DC=R.其中,使得BC=R的有(填正确结论的序号)________. 解:连接OD,
解:连接OD, OC=R
OC=R OC=R
OC=R OC=R
OC=R R,∵OB=R,∴BC=
R,∵OB=R,∴BC= R-R
R-R

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 如图,
如图,

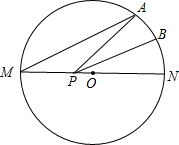 如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为( )
如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为( )