已知菱形ABCD,AB=4,∠ADC=120°,点M在射线AB上,BM=1,∠DMN=60°,射线MN交射线BC于N,则BN=________.
3或5
分析:本题需要分两种情况讨论,①点M在线段AB上,②点M在线段AB的延长线上,根据平行线的性质及解直角三角形的知识,结合相似三角形的性质,分别解出即可.
解答:①当点M在线段AB上时,

过点D作DQ⊥AB于点Q,连接BD,延长DM、CB交于一点P,
则AQ=BQ=2,QM=BM=1,DQ=2

,
在Rt△DQM中,DM=
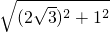
=

,
∵BC∥AD,
∴
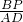
=
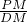
=

=

,
解得:BP=

,PM=
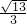
,
∵∠DMN=60°,∠DBC=60°,
∴∠PMN=120°,∠PBD=120°,
∴△PMN∽△PBD,
∴
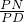
=
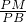
,即
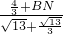
=

,
解得:BN=3;
②当点M在AB延长线上时,

过点D作DQ⊥AB于点Q,连接BD,
则DQ=2

,BD=4,DM=

=

,
∵BP∥AD,
∴
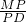
=
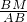
=

,
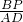
=

=

,
∴BP=

,
又∵MP+PD=DM=

,
∴MP=
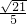
,PD=
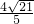
,
∵∠PMN=∠DMN=60°,∠PBD=∠CBD=60°,
∴△PBD∽△PMN,
∴
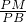
=
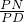
,即
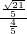
=
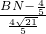
,
解得:BN=5.
综上可得BN=3或5.
故答案为:3或5.
点评:本题考查了菱形的性质,涉及了等腰直角三角形的性质,相似三角形的判定与性质,难度较大,注意构造相似三角形,利用对应边长比例的知识求解.


 ,
,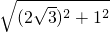 =
= ,
,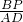 =
=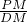 =
= =
= ,
, ,PM=
,PM=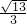 ,
,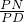 =
=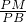 ,即
,即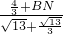 =
= ,
,
 ,BD=4,DM=
,BD=4,DM= =
= ,
,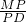 =
=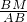 =
= ,
,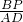 =
= =
= ,
, ,
, ,
,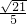 ,PD=
,PD=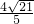 ,
,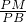 =
=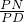 ,即
,即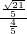 =
=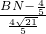 ,
,

