
 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源:同步题 题型:解答题
查看答案和解析>>
科目:初中数学 来源:广东省期中题 题型:解答题
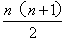 ,即1+2+3+4+…+n=
,即1+2+3+4+…+n=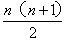 。
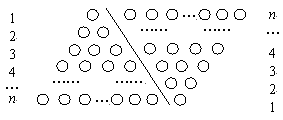
。
查看答案和解析>>
科目:初中数学 来源:期末题 题型:填空题
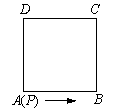
查看答案和解析>>
科目:初中数学 来源:期末题 题型:解答题
| 将正六边形纸片按下列要求分割(每次分割,纸片均不得有剩余);第一次分割:将正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形在分割成一个正六边形和两个全等的正三角形;第二次分割:将第一次分割后所得的正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形再分割成一个正六边形和两个全等的正三角形;按上述分割方法进行下去…… (1)请你在图中画出第一次分割的示意图; | ||||||||||
|
| ||||||||||
| (2)若原正六边形的面积为a,请你通过操作和观察,将第1次,第2次,第3次分割后所得的正六边形的面积填入下表: | ||||||||||
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com