
已知直线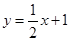 与
与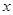 轴交于点
轴交于点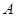 ,与
,与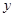 轴交于点
轴交于点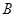 ,将三角形
,将三角形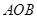 绕点
绕点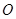 顺时针旋转90°,使点
顺时针旋转90°,使点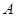 落在点
落在点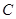 ,点
,点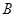 落在点
落在点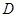 ,抛物线
,抛物线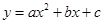 过点
过点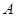 、
、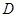 、
、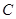 ,其对称轴与直线
,其对称轴与直线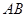 交于点
交于点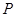 .
.
(1)求抛物线的表达式;
(2)求 的正切值;
的正切值;
(3)点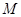 在
在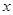 轴上,且△
轴上,且△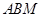 与△
与△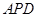 相似,求点
相似,求点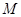 的坐标.
的坐标.
(1)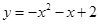 (2)
(2)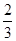 (3)
(3)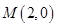 或(
或( ,0)
,0)
【解析】解:(1)由题意得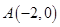 ,
,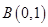
∵△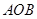 旋转至△
旋转至△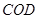 ,∴
,∴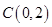 ,
,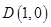 2分
2分
∵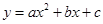 过点
过点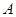 、
、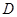 、
、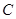 ,
,
∴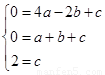 ,
,
∴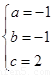 ,即抛物线是
,即抛物线是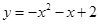 2分
2分
解:(2)设对称轴与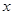 轴交点为
轴交点为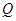 .
.
∵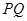 //
// 轴,
轴,
∴∠ =∠
=∠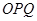
∵抛物线的对称轴为直线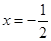 1分
1分
∴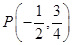 1分
1分
∴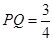 ,
,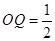 ,在Rt△
,在Rt△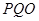 中,
中,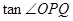 =
=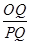 =
=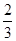
∴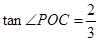 2分
2分
解:(3)∵点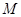 在
在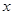 轴上,且△
轴上,且△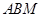 与△
与△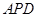 相似,
相似,
∴点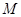 必在点
必在点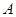 的右侧
的右侧
∵∠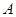 =∠
=∠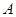 ,
,
∴ 或
或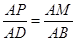 ,
2分
,
2分
即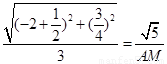 或
或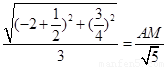 ,
,
∴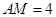 或
或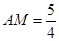
∴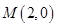 或(
或( ,0)
1分
,0)
1分
(1)先求出点A、B的坐标,再根据旋转的性质求出点C、D的坐标,然后利用待定系数法求抛物线解析式即可;
(2)根据抛物线解析式求出对称轴解析式,然后求出点P的坐标,过点P作PQ⊥x轴,则PQ∥y轴,根据两直线平行,内错角相等可得∠OPQ=∠POC,然后利用点P的坐标,根据锐角的正切值的定义列式计算即可得解;
(3)根据点M在x轴上,且△ABM与△APD相似可知,点M一定在点A的右侧,然后求出AP、AB、AD的长度,因为对应边不明确,所以分①AP和AB是对应边,②AP和AM是对应边,然后根据相似三角形对应边成比例列式求出AM的长度,再根据点A的坐标求解即可.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
已知直线![]() 与
与![]() 轴交于点A(-4,0),与
轴交于点A(-4,0),与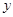 轴交于点B.
轴交于点B.

1.求b的值
2.把△AOB绕原点O顺时针旋转90°后,点A落在![]() 轴的
轴的![]() 处,点B若在
处,点B若在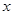 轴的
轴的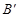 处;
处;
①求直线![]() 的函数关系式;
的函数关系式;
②设直线AB与直线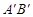 交于点C,矩形PQMN是△
交于点C,矩形PQMN是△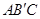 的内接矩形,其中点P,Q在线段
的内接矩形,其中点P,Q在线段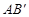 上,点M在线段
上,点M在线段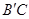 上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
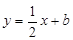 与
与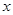 轴交于点A(-4,0),与
轴交于点A(-4,0),与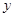 轴交于点B.
轴交于点B.
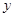 轴的
轴的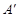 处,点B若在
处,点B若在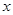 轴的
轴的 处;
处;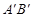 的函数关系式;
的函数关系式;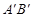 交于点C,矩形PQMN是△
交于点C,矩形PQMN是△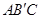 的内接矩形,其中点P,Q在线段
的内接矩形,其中点P,Q在线段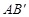 上,点M在线段
上,点M在线段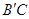 上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.查看答案和解析>>
科目:初中数学 来源:2012届上海市杨浦初三基础测试数学试卷(带解析) 题型:解答题
已知直线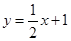 与
与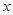 轴交于点
轴交于点 ,与
,与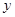 轴交于点
轴交于点 ,将三角形
,将三角形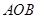 绕点
绕点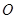 顺时针旋转90°,使点
顺时针旋转90°,使点 落在点
落在点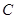 ,点
,点 落在点
落在点 ,抛物线
,抛物线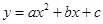 过点
过点 、
、 、
、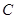 ,其对称轴与直线
,其对称轴与直线 交于点
交于点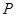 .
.
(1)求抛物线的表达式;
(2)求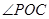 的正切值;
的正切值;
(3)点 在
在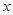 轴上,且△
轴上,且△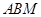 与△
与△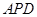 相似,求点
相似,求点 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源:2013届福建省泉州市八年级期中考数学试卷(解析版) 题型:解答题
已知直线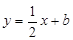 与
与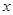 轴交于点A(-4,0),与
轴交于点A(-4,0),与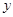 轴交于点B.
轴交于点B.

1.求b的值
2.把△AOB绕原点O顺时针旋转90°后,点A落在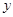 轴的
轴的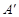 处,点B若在
处,点B若在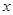 轴的
轴的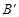 处;
处;
①求直线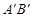 的函数关系式;
的函数关系式;
②设直线AB与直线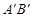 交于点C,矩形PQMN是△
交于点C,矩形PQMN是△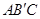 的内接矩形,其中点P,Q在线段
的内接矩形,其中点P,Q在线段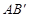 上,点M在线段
上,点M在线段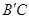 上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com