
【题目】如图,抛物线y=![]() ﹣x﹣4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.
﹣x﹣4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.
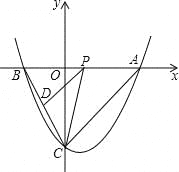
(1)直接写出A、B、C的坐标;
(2)求抛物线y=![]() ﹣x﹣4的对称轴和顶点坐标;
﹣x﹣4的对称轴和顶点坐标;
(3)求△PCD面积的最大值,并判断当△PCD的面积取最大值时,以PA、PD为邻边的平行四边形是否为菱形.
【答案】(1)A(4,0)、B(﹣2,0)、C(0,﹣4).(2)(1,﹣![]() )(3)不是菱形
)(3)不是菱形
【解析】试题分析:(1)设y=0,解一元二次方程即可求出A和B的坐标,设x=0,则可求出C的坐标.
(2)抛物线:y=![]() x2-x-4=
x2-x-4=![]() (x-1)2-
(x-1)2-![]() ,所以抛物线的对称轴是直线x=1,顶点坐标是(1,-
,所以抛物线的对称轴是直线x=1,顶点坐标是(1,-![]() ).
).
(3)设P(x,0)(-2<x<4),由PD∥AC,可得到关于PD的比例式,由此得到PD和x的关系,再求出C到PD的距离(即P到AC的距离),利用三角形的面积公式可得到S和x的函数关系,利用函数的性质即可求出三角形面积的最大值,进而得到x的值,所以PD可求,而PA≠PD,所以PA、PD为邻边的平行四边形不是菱形.
试题解析:(1)A(4,0)、B(-2,0)、C(0,-4).
(2)抛物线:y=![]() x2-x-4=
x2-x-4=![]() (x-1)2-
(x-1)2-![]() ,
,
∴抛物线的对称轴是直线x=1,顶点坐标是(1,-![]() ).
).
(3)设P(x,0)(-2<x<4),
∵PD∥AC,
∴![]() ,
,
解得:PD=![]() (x+2),
(x+2),
∵C到PD的距离(即P到AC的距离):d=PA×sin450=![]() (4-x),
(4-x),
∴△PCD的面积S=![]() ×PD×d=
×PD×d=![]() (x+2)(4-x)="-"
(x+2)(4-x)="-"![]() x2+
x2+![]() x+
x+![]() ,
,
∴S=-![]() (x-1)2+3,
(x-1)2+3,
∴△PCD面积的最大值为3,
当△PCD的面积取最大值时,x=1,PA=4-x=3,PD=![]() (x+2)=2
(x+2)=2![]() ,
,
因为PA≠PD,所以以PA、PD为邻边的平行四边形不是菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在2019年广东省政府工作报告中指出:我省大力实施乡村振兴战略,加快解决农业农村突出问题,“三农”工作取得新成效,省财政自2018年起三年投入75亿元支持粤东粤西粤北省级现代农业产业园建设.用科学记数法表示75亿为( )
A. 7.5×108B. 0.75×1010C. 75×108D. 7.5×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中, 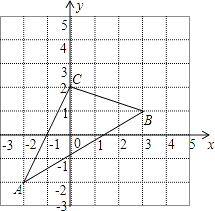
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;
(2)求售价x的范围;
(3)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com