
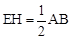 ;
;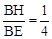 ,求
,求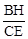 的值.
的值.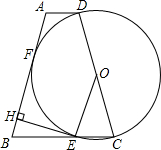
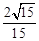 .
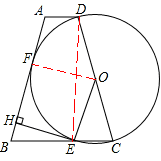
.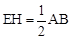 ,只需证明四边形OEHF是平行四边形,要证明OEHF是平行四边形,已知它有一组对边平行,只需再说明另一组对边平行,由已知EH⊥AB和圆切线的性质即可得到.
,只需证明四边形OEHF是平行四边形,要证明OEHF是平行四边形,已知它有一组对边平行,只需再说明另一组对边平行,由已知EH⊥AB和圆切线的性质即可得到.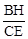 ,只要证明△EHB∽△DEC,再根据相似三角形的性质来求即可.
,只要证明△EHB∽△DEC,再根据相似三角形的性质来求即可.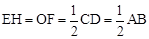 .
.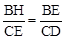 .
.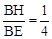 ,设
,设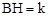 ,则
,则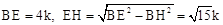 ,
, 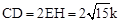 . ∴
. ∴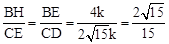 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:单选题
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.甲、乙均正确 | B.甲、乙均错误 |
| C.甲正确,乙错误 | D.甲错误,乙正确 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
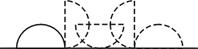
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .若动点D在线段AC上(不与点A、C重合),过点D作DE⊥AC交AB边于点E.
.若动点D在线段AC上(不与点A、C重合),过点D作DE⊥AC交AB边于点E.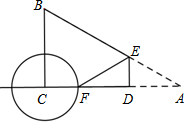
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
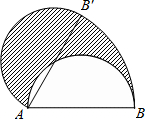
A.6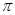 | B.5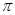 | C.4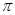 | D.3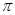 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com