
如图在平面直角坐标系内,以点C(1,1)为圆心,2为半径作圆,交x轴于A、B两点,开口向下的抛物线经过A、B两点,且其顶点P在⊙C上。
(1)写出A、B两点的坐标;
(2)确定此抛物线的解析式;
(1) A(1-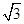 ,0),B(1+
,0),B(1+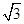 ,0);(2)y=-x2+2x+2.
,0);(2)y=-x2+2x+2.
解析试题分析:(1)过C作AB的垂线,设垂足为H,在Rt△CAH中,已知圆的半径和CH的长(由C点坐标获得),利用勾股定理即可求得AH的长,进而可得到点A的坐标,B点坐标的求法相同.
(2)根据抛物线和圆的对称性知:C、P都在弦AB的垂直平分线上,已知了C点坐标和圆的半径,即可得到点P的坐标,而P为抛物线顶点,可将所求抛物线设为顶点坐标式,然后将A点坐标代入抛物线的解析式中,即可求得待定系数的值,从而求出该抛物线的解析式.
试题解析:(1)过点C作CH⊥x轴,H为垂足;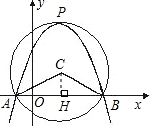
又∵C(1,1),
∴CH=OH=1;(1分)
∴在Rt△CHB中,HB=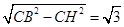 ;
;
∵CH⊥AB,CA=CB,
∴AH=BH;
故A(1-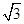 ,0),B(1+
,0),B(1+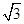 ,0).
,0).
(2)由圆与抛物线的对称性可知抛物线的顶点P的坐标为(1,3);
∴设抛物线解析式为y=a(x-1)2+3,
由已知得抛物线经过点B(1+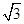 ,0),
,0),
把点B(1+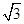 ,0)代入上式,
,0)代入上式,
解得a=-1,
∴抛物线的解析式为:y=-x2+2x+2.
考点: 二次函数综合题


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:解答题
如图,矩形ABCD的两边长AB=18 cm,AD=4 cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2 cm的速度匀速运动,Q在边BC上沿BC方向以每秒1 cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线 与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.
与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.
(1)说明: ;
;
(2)当点C、点A到y轴距离相等时,求点E坐标.
(3)当 的面积为
的面积为 时,求
时,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: .
.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,AB在x轴上,以AB为直径的半⊙O’与y轴正半轴交于点C,连接BC,AC.CD是半⊙O’的切线,AD⊥CD于点D.
(1)求证:∠CAD =∠CAB;
(2)已知抛物线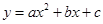 过A、B、C三点,AB=10,tan∠CAD=
过A、B、C三点,AB=10,tan∠CAD= .
.
① 求抛物线的解析式;
② 判断抛物线的顶点E是否在直线CD上,并说明理由;
③ 在抛物线上是否存在一点P,使四边形PBCA是直角梯形.若存在,直接写出点P的坐标(不写求解过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了改善市民的生活环境,我市在某河滨空地处修建一个如图所示的休闲文化广场.在Rt△内修建矩形水池,使顶点、在斜边上,、分别在直角边、上;又分别以、、为直径作半圆,它们交出两弯新月(图中阴影部分),两弯新月部分栽植花草;其余空地铺设地砖.其中 ,
, .设
.设 米,
米, 米.
米.
(1)求 与
与 之间的函数解析式;
之间的函数解析式;
(2)当 为何值时,矩形的面积最大?最大面积是多少?
为何值时,矩形的面积最大?最大面积是多少?
(3)求两弯新月(图中阴影部分)的面积,并求当 为何值时,矩形的面积等于两弯新月面积的
为何值时,矩形的面积等于两弯新月面积的 ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.
(1)填表:(不需化简)
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | | 40 |
| 销售量(件) | 200 | | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐上,且点A(0,2),点C( ,0),如图所示:抛物线
,0),如图所示:抛物线 经过点B。
经过点B。
(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线的解析式为
(1)求证:不论m为何值,此抛物线与x轴必有两个交点,且两交点A、B之间的距离为定值;
(2)设点P为此抛物线上一点,若△PAB的面积为8,求符合条件的点P的坐标;
(3)若(2)中△PAB的面积为S(S>0),试根据面积S值的变化情况,确定符合条件的点P的个数(本小题直接写出结论,不要求写出计算、证明过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com