
 把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=35°,则下面五个结论:①∠CEF=35°;②∠AEC=145°;③∠BGE=70°;④∠EFD′=110°;⑤∠D′FD=70°.其中正确的是①③⑤.(只填序号)
把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=35°,则下面五个结论:①∠CEF=35°;②∠AEC=145°;③∠BGE=70°;④∠EFD′=110°;⑤∠D′FD=70°.其中正确的是①③⑤.(只填序号) 分析 根据折叠得出∠C′EF=∠CEF,∠EFD=∠EFD′,根据平行线的性质求出∠EFB=∠C′EF=32°,∠D′FD=∠FGC,再逐个判断即可.
解答 解:∵AE∥BG,∠EFB=35°,
∴∠C′EF=∠EFB=35°,
根据折叠得:∠CEF=∠C′EF=35°,∴①正确;
∵根据折叠得:∠CEF=∠C′EF=35°,
∴∠AEC=180°-35°-35°=110°,∴②错误;
∵∠EFB=∠CEF=35°,
∴∠BGE=35°+35°=70°,∴③正确;
∵∠EFB=35°,
∴∠EFD′=180°-35°=145°,∴④错误;
∵∠BGE=70°,
∴∠FGC=∠BGE=70°,
∵CE∥FD,
∴∠D′FD=∠FGC=70°,∴⑤正确;
故答案为:①③⑤.
点评 本题考查了折叠的性质和平行线的性质等知识点,能灵活运用性质进行推理是解此题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的高不可能是( )
如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的高不可能是( )| A. | 4 | B. | $\sqrt{15}$ | C. | $\sqrt{7}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
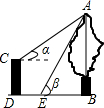 学习完解直角三角形知识,同学们利用它求我校某平房前一棵大树的高度,如图,大树AB与平房CD底部在同一平地,知道二层平房CD高为6米,在平房顶部点C测得树顶A点的仰角α=30°,从平房底部向树的方向水平前进2米到达点E,在点E处测得大树顶A的仰角β=60°,请你帮同学们求出这棵大树高度AB(结果保留根号)
学习完解直角三角形知识,同学们利用它求我校某平房前一棵大树的高度,如图,大树AB与平房CD底部在同一平地,知道二层平房CD高为6米,在平房顶部点C测得树顶A点的仰角α=30°,从平房底部向树的方向水平前进2米到达点E,在点E处测得大树顶A的仰角β=60°,请你帮同学们求出这棵大树高度AB(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com