
 如图,两圆半径均为1,且图中两阴影部分的面积相等,那么OC的长度是________.
如图,两圆半径均为1,且图中两阴影部分的面积相等,那么OC的长度是________.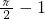
 π=[(1+x)÷2]×1,解之即可求解.
π=[(1+x)÷2]×1,解之即可求解. 解:如图,设两圆相交于点S,E点延长ES交于AB于点F,OO1交于ES于点W,
解:如图,设两圆相交于点S,E点延长ES交于AB于点F,OO1交于ES于点W, π=[(1+x)÷2]×1,
π=[(1+x)÷2]×1, -1.
-1.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com