|
|
|
如图(1),在正方形ABCD中,E,F分别是边AD、DC上的点,且AF⊥BE.
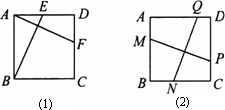
(1)求证:AF=BE.
(2)如图(2),在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?请说明理由.
|
|
|
答案:
解析:
|
(1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,
∴∠DAF+∠BAF=90°,
∵AF⊥BE,
∴∠ABE+∠BAF=90°,
∴∠ABE=∠DAF.
在△ABE和△DAF中,
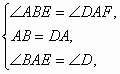
∴△ABE≌△DAF,
∴AF=BE.
(2)解:MP与NQ相等.
理由如下:过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,
则AF=MP,BE=NQ.
同(1)可证△AFD≌△BEA,
∴AF=BE,
∴MP=NQ.
|
练习册系列答案
相关习题
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
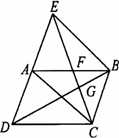
如图所示,已知在平行四边形ABCD中,E是边DA的延长线上一点,且AE=AD,连接EC,分别交AB、BD于点F、G,证明:AF=BF.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
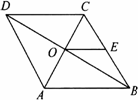
如图,在菱形ABCD中,对角线AC、BD交于点O,AB=8,E是BC的中点,则OE的长等于________.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
如图,在□ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于G、H,给出下列结论:
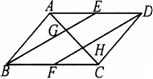
①△ABE≌△CDF;
②AG=GH=HC;
③ ; ;
④S△ABE=2S△AGB.其中正确的结论有________个.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
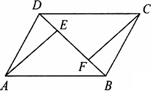
如图,已知在平行四边形ABCD中,E、F为对角线BD上的两点且BE=DF,连接AE、CF.求证:AE=CF.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
已知四边形ABCD中,AD∥BC.要判定四边形ABCD是平行四边形,则还需满足条件
|
| [ ] |
A. |
∠A+∠C=180°
|
B. |
∠B+∠D=180°
|
C. |
∠B+∠A=180°
|
D. |
∠A+∠D=180°
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
计算: . .
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
如果△ABC的三边长分别为m2-1,2 m,m2+1,其中m为大于1的正整数,则
|
| [ ] |
A. |
△ABC是直角三角形,且斜边为m2-1
|
B. |
△ABC是直角三角形,且斜边为2 m
|
C. |
△ABC是直角三角形,且斜边为m2+1
|
D. |
△ABC不是直角三角形
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
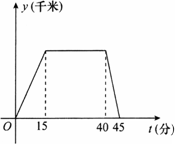
如图所示是邻居张大爷去公园锻炼及原路返回时离家的距离y(千米)与时间t(分)之间的函数图象,根据图象信息知,下列说法正确的是
|
| [ ] |
A. |
张大爷去时所用的时间少于回家所用的时间
|
B. |
张大爷在公园锻炼了40分钟
|
C. |
张大爷去时走下坡路,回家时走上坡路
|
D. |
张大爷去时的速度比回家时的速度慢
|
|
|
查看答案和解析>>

 备战中考寒假系列答案
备战中考寒假系列答案