
分析 根据题目中的信息,我们可以求得等腰三角形底边上的高,然后根据等积法可以求得腰上的高.
解答 解:设底边上的高为12x,则腰长为13x.
∵在等腰三角形中,底边长为10m,
∴底边上的高也是底边的中线,则底边的一半是5m.
∴勾股定理可得,52+(12x)2=(13x)2.
解得,x=1.
∴底边上的高为12,腰长为13.
∴此等腰三角形的面积为:$\frac{10×12}{2}=60{m}^{2}$.
设腰上的高为y,则
$\frac{13×y}{2}=60$.
解得y=$\frac{120}{13}m$.
即此等腰三角形的面积为60m2,腰上的高为$\frac{120}{13}m$.
点评 本题考查解直角三角形和等积法,关键是明确等积法是指的同一个三角形,每条边和它上的高的乘积除以2的结果都相等.


科目:初中数学 来源: 题型:解答题
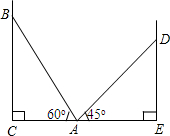 在两面墙之间有一个低端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=$\sqrt{18}$m.
在两面墙之间有一个低端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=$\sqrt{18}$m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
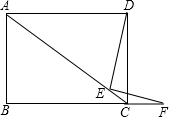 如图:四边形ABCD为矩形,E在对角线AC上,F在边BC的延长线上,且$\frac{DE}{EF}$=$\frac{BC}{AB}$,求证:DE⊥EF.
如图:四边形ABCD为矩形,E在对角线AC上,F在边BC的延长线上,且$\frac{DE}{EF}$=$\frac{BC}{AB}$,求证:DE⊥EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 桌子张数 | 4 | 5 | … | n |
| 可坐人数 | 12 | 14 | … | 4+2n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com