
25.(本小题满分14分)
 如图13,二次函数
如图13,二次函数![]() 的图象与x轴交于A、B两点,与y轴交于点C(0,-1),ΔABC的面积为
的图象与x轴交于A、B两点,与y轴交于点C(0,-1),ΔABC的面积为![]() 。
。
(1)求该二次函数的关系式;
(2)过y轴上的一点M(0,m)作y轴上午垂线,若该垂线与ΔABC的外接圆有公共点,求m的取值范围;
(3)在该二次函数的图象上是否存在点D,使四边形ABCD为直角梯形?若存在,求出点D的坐标;若不存在,请说明理由。
解:(1)OC=1,所以,q=-1,又由面积知0.5OC×AB=![]() ,得AB=
,得AB=![]()
设A(a,0),B(b,0)
AB=b-a=![]()
![]() =
=![]() ,解得p=
,解得p=![]() ,但p<0,所以p=
,但p<0,所以p=![]() 。
。
所以解析式为:![]()
(2)令y=0,解方程得![]() ,得
,得![]() ,所以A(
,所以A(![]() ,0),B(2,0),在直角三角形AOC中可求得AC=
,0),B(2,0),在直角三角形AOC中可求得AC=![]() ,同样可求得BC=
,同样可求得BC=![]() ,,显然AC2+BC2=AB2,得三角形ABC是直角三角形。AB为斜边,所以外接圆的直径为AB=
,,显然AC2+BC2=AB2,得三角形ABC是直角三角形。AB为斜边,所以外接圆的直径为AB=![]() ,所以
,所以![]() .
.
(3)存在,AC⊥BC,①若以AC为底边,则BD//AC,易求AC的解析式为y=-2x-1,可设BD的解析式为y=-2x+b,把B(2,0)代入得BD解析式为y=-2x+4,解方程组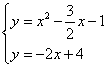 得D(
得D(![]() ,9)
,9)
②若以BC为底边,则BC//AD,易求BC的解析式为y=0.5x-1,可设AD的解析式为y=0.5x+b,把 A(![]() ,0)代入得AD解析式为y=0.5x+0.25,解方程组
,0)代入得AD解析式为y=0.5x+0.25,解方程组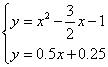 得D(
得D(![]() )
)
综上,所以存在两点:(![]() ,9)或(
,9)或(![]() )。
)。


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
(2011广西崇左,25,14分)(本小题满分14分)已知抛物线y=x2+4x+m(m为常数)
经过点(0,4).
(1) 求m的值;
(2) 将该抛物线先向右、再向下平移得到另一条抛物线.已知平移后的抛物线满足下述两个条件:它的对称轴(设为直线l2)与平移前的抛物线的对称轴(设为直线l1)关于y轴对称;它所对应的函数的最小值为-8.
① 试求平移后的抛物线的解析式;
② 试问在平移后的抛物线上是否存在点P,使得以3为半径的圆P既与x轴相切,又与直线l2相交?若存在,请求出点P的坐标,并求出直线l2被圆P所截得的弦AB的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
 与y轴交于点C(0,
与y轴交于点C(0, ), 与x轴交于点A、 B,点A的坐标为(2,0).
), 与x轴交于点A、 B,点A的坐标为(2,0).
 与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(
与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为( ,0).问:是否存在这样的直线
,0).问:是否存在这样的直线 ,使得△OMF是等腰三角形?若存 在,请求出点Q的坐标;若不存在,请说明理由.
,使得△OMF是等腰三角形?若存 在,请求出点Q的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2011年广东省萝岗区初中毕业班综合测试数学卷 题型:解答题
(本小题满分14分)
如图1,抛物线 与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线
与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线 与抛物线交于点B、C.
与抛物线交于点B、C.
【小题1】(1)求点A的坐标;
【小题2】(2)当b=0时(如图2),求 与
与 的面积。
的面积。
【小题3】(3)当 时,
时, 与
与 的面积大小关系如何?为什么?
的面积大小关系如何?为什么?
【小题4】(4)是否存在这样的b,使得 是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(内蒙古赤峰卷)数学 题型:解答题
(2011广西崇左,25,14分)(本小题满分14分)已知抛物线y=x2+4x+m(m为常数)
经过点(0,4).
(1) 求m的值;
(2) 将该抛物线先向右、再向下平移得到另一条抛物线.已知平移后的抛物线满足下述两个条件:它的对称轴(设为直线l2)与平移前的抛物线的对称轴(设为直线l1)关于y轴对称;它所对应的函数的最小值为-8.
① 试求平移后的抛物线的解析式;
② 试问在平移后的抛物线上是否存在点P,使得以3为半径的圆P既与x轴相切,又与直线l2相交?若存在,请求出点P的坐标,并求出直线l2被圆P所截得的弦AB的长度;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com