
 ,动点P、Q分别在AB、OB上运动,运动时,始终保持∠OPQ=45°不变,设PA=x,OQ=y.
,动点P、Q分别在AB、OB上运动,运动时,始终保持∠OPQ=45°不变,设PA=x,OQ=y.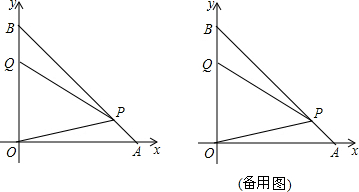
 ,试探究:当点P从点A出发第一次运动到点D时,点Q运动的路径长为多少?
,试探究:当点P从点A出发第一次运动到点D时,点Q运动的路径长为多少? ,
, -y,
-y, =
= ,即
,即 =
= ,
, .
.
 ,0);
,0);
 ,
, );
);
 ,AP=AB-BP=2-
,AP=AB-BP=2- ,
, =
= -1,AE=
-1,AE= -1,OE=OA-AE=1,
-1,OE=OA-AE=1, -1);
-1); )或(
)或(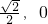 )或(
)或(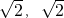 ).
).
 ,
, ,
, ,
, =
= ,
, 时,y3=
时,y3= ,
,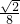 ,
, +
+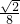 =
= .
.

科目:初中数学 来源: 题型:
 17、如图,D、E两点分别在AC、AB上,且DE与BC不平行,请填上一个你认为合适的条件:
17、如图,D、E两点分别在AC、AB上,且DE与BC不平行,请填上一个你认为合适的条件:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,A,B两点分别位于一个池塘的两端,小聪想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点M,N,并且测出MN的长为10m,则A,B间的距离为
如图,A,B两点分别位于一个池塘的两端,小聪想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点M,N,并且测出MN的长为10m,则A,B间的距离为查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,A、B两点分别位于池塘两侧,小亮用下面的方法测量A、B之间的距离,先在地上取一个可以直接到达A点和B点的C点,连接AC、BC,并分别延长至D、E两点,使DC=AC,EC=BC,那么量出DE的长就是A、B间的距离,请说明一下这样做的道理.
如图,A、B两点分别位于池塘两侧,小亮用下面的方法测量A、B之间的距离,先在地上取一个可以直接到达A点和B点的C点,连接AC、BC,并分别延长至D、E两点,使DC=AC,EC=BC,那么量出DE的长就是A、B间的距离,请说明一下这样做的道理.查看答案和解析>>
科目:初中数学 来源: 题型:
 问题解决.
问题解决.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com