Question

已知直角坐标平面内的△ABC三个顶点A、B、C的坐标分别为（4，3）、（1，2）、（3，-4），则△ABC的形状是________．

Answer 1

直角三角形
分析：首先根据两点间的距离公式求出AB，BC，AC的长度，然后根据勾股定理的逆定理即可确定该三角形为直角三角形．
解答：∵点A、B、C的坐标分别为（4，3）、（1，2）、（3，-4），
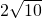
∴AB=，BC=，AC=5，
∴AC²=AB²+BC²，
∴△ABC为直角三角形，
故答案为直角三角形．
点评：本题主要考查勾股定理的逆定理、两点间的距离公式，关键在于正确的计算出AB，BC，AC的长度，正确的运用相关的定理、公式．