
【题目】阅读下面材料:
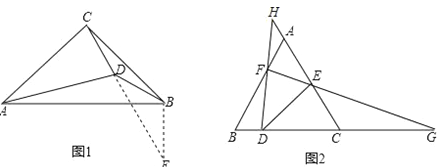
小明遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,AC=BC,在三角形内取一点D,AD=AC,∠CAD=30°,求∠ADB.
小明通过探究发现,∠DAB=∠DCB=15°,BC=AD,这样就具备了一边一角的图形特征,他果断延长CD至点E,使CE=AB,连接EB,造出全等三角形,使问题得到解决.
(1)按照小明思路完成解答,求∠ADB;
(2)参考小明思考问题的方法,解答下列问题:
如图2,△ABC中,AB=AC,点D、E、F分别为BC、AC、AB上一点,连接DE,延长FE、DF分别交BC、CA延长线于点G、H,若∠DHC=∠EDG=2∠G.
①在图中找出与∠DEC相等的角,并加以证明;
②若BG=kCD,猜想DE与DG的数量关系并证明.
【答案】(1)135°;(2)①∠HDC=∠DEC;②猜想DG=kDE.
【解析】
(1)根据辅助线证得△DAB≌△BCE,则∠ADB=∠CBE(还不能直接求得,考虑全等的其他等边等角),∠ABD=∠E,BD=BE,得到∠BDE=∠E=∠ABD.考虑引入未知数,设∠CBD=x,则∠E=∠ABD=∠BDE=x+15°,利用∠ABC=∠ABD+∠CBD求得x,再由周角求得结果.
(2)①∠DEC是△DEH的外角,等于∠DHC+∠HDE,而∠DHC=∠EDG,等量代换得∠DEC=∠EDG+∠HDE=∠HDC.
②由条件DHC=∠EDG=2∠G,在FG上方构造2∠G即∠FGM=∠FGD,则∠EDG=∠MGD,令M落在BA延长线上,加上∠B=∠ACB,即得△BGM∽△CDE,有![]() =k.又通过三角形内角和求得∠M=∠HDC,证得△MFG≌△DFG,有MG=DG,得证.
=k.又通过三角形内角和求得∠M=∠HDC,证得△MFG≌△DFG,有MG=DG,得证.
(1)延长CD至点E,使CE=AB,连接EB
∵,∠ACB=90°,AC=BC
∴∠CAB=∠CBA=45°
∵AD=AC,∠CAD=30°
∴BC=AD,∠ACD=∠ADC=![]() =75°,∠DAB=∠CAB﹣∠CAD=15°
=75°,∠DAB=∠CAB﹣∠CAD=15°
∴∠BCD=∠ACB﹣∠ACD=15°
即∠DAB=∠BCD
在△DAB与△BCE中,

∴△DAB≌△BCE(SAS)
∴∠ADB=∠CBE,∠ABD=∠E,BD=BE
∴∠BDE=∠E
设∠CBD=x,则∠ABD=45°﹣x,∠BDE=∠BCD+∠CBD=15°+x
∴∠ABD=∠E=∠BDE=15°+x
∵∠ABC=∠ABD+∠CBD
∴45°=15°+x+x,得:x=15°
∴∠CDB=180°﹣∠BCD﹣∠CBD=180°﹣15°﹣15°=150°
∴∠ADB=360°﹣∠ADC﹣∠CDB=360°﹣75°﹣150°=135°
(2)①∠HDC=∠DEC,证明如下:
∵∠DHC=∠EDG
∴∠HDC=∠HDE+∠EDG=∠HDE+∠DHC=∠DEC
∴∠HDC=∠DEC
②猜想DG=kDE,证明如下:
在FG的上方作∠FGM=∠FGD,使∠FGM的一边与BA延长线交于M
∵∠DHC=∠EDG=2∠FGD
∴∠DHC=∠EDG=∠MGD
∵AB=AC
∴∠B=∠ACB
∴∠M=180°﹣∠B﹣∠MGD=180°﹣∠ACB﹣∠EDC=∠DEC
∴∠M=∠HDC
在△MFG与△DFG中,
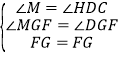
∴△MFG≌△DFG(AAS)
∴MG=DG
∵∠B=∠ACB,∠EDG=∠MGD
∴△BGM∽△CDE
∴![]()
∵BG=kCD
∴![]() =K
=K
∴DG=MG=kDE


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
①4a+c<0;②m(am+b)+b>a(m≠﹣1);③关于x的一元二次方程ax2+(b﹣1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 “低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了某单位员工上下班的交通方式,绘制了如下统计图:

(1)填空:样本中的总人数为 ;开私家车的人数m= ;扇形统计图中“骑自行车”所在扇形的圆心角为 度;
(2)补全条形统计图;
(3)该单位共有2000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行,坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?
查看答案和解析>>
科目:初中数学 来源: 题型:
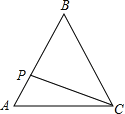
【题目】如图,正△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿![]() 的方向运动,到达点C时停止,设运动时间为x(秒),
的方向运动,到达点C时停止,设运动时间为x(秒),![]() ,则y关于x的函数的图像大致为( )
,则y关于x的函数的图像大致为( )
A. 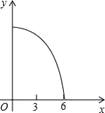 B.
B. 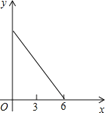 C.
C. 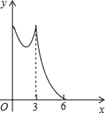 D.
D. 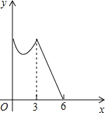
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂大门是一抛物线形水泥建筑物(如图),大门地面宽AB=4米,顶部C离地面高度为4.4米.现有一辆满载货物的汽车欲通过大门,货物顶部距地面2.8米,装货宽度为2.4米.请通过计算,判断这辆汽车能否顺利通过大门?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一间摄影展览厅,其东、西面各有一个入口A、B,南面为出口C,北面分别有两个出口D、E,摄影爱好者郑浩任选一个入口进入展览厅,参观结束后,任选一个出口离开。
(1)郑浩从进入到离开共有多少种可能的结果?请画出树形图;
(2)求出郑浩从入口A进入展览厅并从北面出口离开的概率。

查看答案和解析>>
科目:初中数学 来源: 题型:
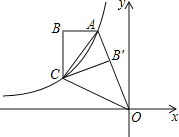
【题目】如图,双曲线y=![]() (x<0)经过Rt△ABC的两个顶点A,C,∠ABC=90°,AB∥x轴,连接OA,将Rt△ABC沿AC翻折后得到Rt△AB′C,点B′刚好落在线段OA上,连接OC,OC恰好平分OA与x轴负半轴的夹角,若Rt△ABC的面积为2,则k的值为___.
(x<0)经过Rt△ABC的两个顶点A,C,∠ABC=90°,AB∥x轴,连接OA,将Rt△ABC沿AC翻折后得到Rt△AB′C,点B′刚好落在线段OA上,连接OC,OC恰好平分OA与x轴负半轴的夹角,若Rt△ABC的面积为2,则k的值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F、G分别为边AB、BC、AD上的中点,连接AF、DE交于点M,连接GM、CG,CG与DE交于点N,则结论①GM⊥CM;②CD=DM;③四边形AGCF是平行四边形;④∠CMD=∠AGM中正确的有( )个.
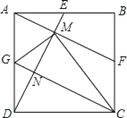
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了以“责任、感恩”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图,

(1)该班有 人,学生选择“和谐”观点的有 人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是 度;
(2)如果该校有360名初三学生,利用样本估计选择“感恩”观点的初三学生约有 人;
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com