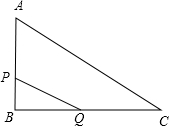
解:(1)∵P、Q移动t秒时AP=t,BQ=2t,
则PB=AB-AP=6-t,
∴S
△PBQ=

,
∵S
△ABC=
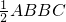
=
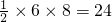
,
当S
△PBQ=

S
△ABC时,则t(6-t)=

,
t
2-6t+8=0,
t
1=2,t
2=4,
∴当t=2或4时,△PBQ的面积等于△ABC的面积的

.
(2)不存在t的值,得△PQB的面积等于10cm
2.
理由:设S
△PQB=10,由(1)知:S
△PBQ=t(6-t),
∴t(6-t)=10,整理得t
2-6t+10=0,
∵△=(-6)
2-4×1×10=-4<0,
∴该方程无解,
∴不存在t的值,使得△PQB的面积等于10cm
2.
(3)当PQ=6时,在Rt△PBQ中,∵BP
2+BQ
2=PQ
2,
∴(6-t)
2+(2t)
2=6
2,
5t
2-12t=0,
t(5t-12)=0,
t
1=0,t
2=

,
∵t=0时不合题意,舍去,
∴当t=

时,PQ的长度等于6cm.
(4)当PQ∥AC时,则△BPQ∽△BAC,
∴

,
∴

整理得3t=12-2t,
∴t=

,
∴当t=

时,PQ∥AC.
分析:(1)首先表示出AP=t,BQ=2t,PB=AB-AP=6-t,再得出S
△PBQ与S
△ABC面积,利用S
△PBQ=

S
△ABC求出即可;
(2)利用S
△PBQ=t(6-t),假设等于10,利用根的判别式求出即可;
(3)根据PQ=6,利用勾股定理BP
2+BQ
2=PQ
2,求出即可;
(4)当PQ∥AC时,则△BPQ∽△BAC,得出对应边的关系,再求出t即可.
点评:此题主要考查了一元二次方程的应用以及相似三角形的判定与性质、三角形面积求法等知识,此题涉及知识较多,难度不大,关键是要对知识的熟练应用.

 ?
?
 ,
,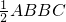 =
=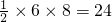 ,
, S△ABC时,则t(6-t)=
S△ABC时,则t(6-t)= ,
, .
. ,
, 时,PQ的长度等于6cm.
时,PQ的长度等于6cm. ,
, 整理得3t=12-2t,
整理得3t=12-2t, ,
, 时,PQ∥AC.
时,PQ∥AC. S△ABC求出即可;
S△ABC求出即可;

 全能测控期末小状元系列答案
全能测控期末小状元系列答案