
| 1 | 2 |
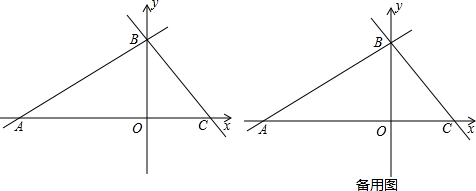
| 2 |
| 1 |
| 2 |
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
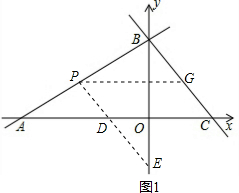 ∴PG=-
∴PG=-| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 2 |
3
| ||
| 2 |
| 2 |
| 14 |
| 3 |
| 3 |
| 2 |
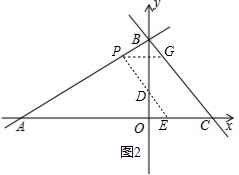
| 2 |
3
| ||
| 2 |
| 2 |
| 14 |
| 3 |
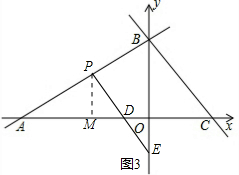 ∴P(m,
∴P(m,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
3
| ||
| 2 |
| 2 |
| 14 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
3
| ||
| 2 |
| 2 |
| 14 |
| 3 |
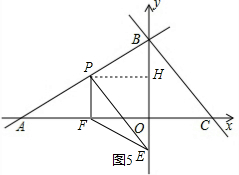 ∴PE=-m,
∴PE=-m,| PF |
| BC |
| PE |
| AC |
| ||
7
|
-
| ||
| 21 |
| PF |
| AC |
| PE |
| BC |
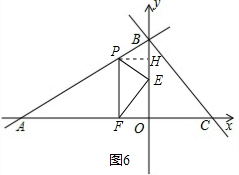 ∴
∴
| ||
| 21 |
-
| ||
7
|


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•道外区一模)如图,在△ABC中,AB=AC,∠ABC=40°,把△ABC绕点A逆时针旋转20°得到△ADE(点D与点B是对应点,点E与点C是对应点),连接BD,则∠DBC的度数为( )
(2013•道外区一模)如图,在△ABC中,AB=AC,∠ABC=40°,把△ABC绕点A逆时针旋转20°得到△ADE(点D与点B是对应点,点E与点C是对应点),连接BD,则∠DBC的度数为( )查看答案和解析>>
科目:初中数学 来源: 题型:
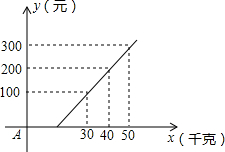 (2013•道外区一模)如图所示,是某航空公司托运行李的费用y(元)与行李重量x(千克)的关系图象,由图中可知,乘客可以免费托运行李的最大重量为( )
(2013•道外区一模)如图所示,是某航空公司托运行李的费用y(元)与行李重量x(千克)的关系图象,由图中可知,乘客可以免费托运行李的最大重量为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com