Question

14．在平面直角坐标系中，O为坐标原点，直线y=-x+c与x轴交于点B，与y轴交于点C，抛物线y=a（x+1）（x-3）经过B、C两点，与x轴交于另一点A．
（1）如图l，求a的值；
（2）如图2，点P在第一象限的抛物线上，连接AP交y轴于点D，交直线BC于点E，当PE=AD时，求点P的坐标；
（3）如图3，在（2）的条件下，点Q在第二象限的抛物线上，QF⊥x轴于点F，点G在线段OB上，OG=2OF，PG交BQ于点H，交BC于点M，若∠QHG-2∠GBH=45°，求点Q的坐标．

Answer 1

分析 （1）根据交点式可求得抛物线与x轴的两个交点坐标，代入一次函数中可得C的坐标，从而得出a的值；
（2）如图2，作辅助线，构建全等的直角三角形PEK，得EK=OA=1，根据抛物线的解析式设P点的横坐标为t，则P点的纵坐标为：（t+1）（3-t），由A（-1，0）在直线AP上得：解析式为y=kx+k，列式为：kt+k=（t+1）（3-t），k=3-t，表示直线AP的解析式，并写出D的坐标（0，3-t），从而表示E的坐标[t-1，（t-1）（3-t）+（3-t）]，即E[t-1，t（3-t）]，因为点E在直线y=-x+3上，代入可求得t的值，写P的坐标；
（3）如图3，作辅助线，构建直角三角形，设OF=m，则OG=2m，根据抛物线的解析式表示点Q的坐标为[-m，（1-m）（3+m）]，得FQ=（1-m）（3+m），FB=3+m，所以tan∠QBF=$\frac{FQ}{FB}$=1-m，利用三角形外角定理得：∠QHG=∠GBH+∠PAB+∠APG，与已知∠QHG-2∠GBH=45°相结合，得∠APG=∠GBH，列式：tan∠APG=$\frac{NG}{PN}$=$\frac{\frac{\sqrt{2}}{2}（2m+1）}{\frac{5\sqrt{2}}{2}-\sqrt{2}m}$=1-m，求出m的值，因为QF⊥x轴于点F，则OF＜OA，对m的值进行取舍得：m=$\frac{1}{2}$，代入可得Q的坐标．

解答 解：（1）由a（x+1）（x-3）=0得：A（-1，0），B（3，0），
把B（3，0）代入y=-x+c中得：c=3，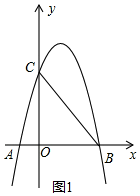
∴C（0，3），
由y=a（x+1）（x-3）得：C（0，-3a），
∴-3a=3，
a=-1；

（2）如图2，过点E作EK∥x轴，过点P作PK⊥EK，
∴∠PEK=∠DAO，∠PKE=∠DOA=90°，
∵PE=AD，
∴△AOD≌△EKP，
∴EK=OA，PK=OD，
∴A（-1，0），
∴EK=OA=1，
设P点的横坐标为t，则P点的纵坐标为：（t+1）（3-t），
∵A（-1，0），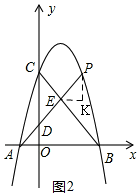
∴直线AP的解析式为：y=kx+k，
∴kt+k=（t+1）（3-t），
即k（t+1）=（t+1）（3-t），
∵t+1＞0，
∴k=3-t，
∴直线AP的解析式为：y=（3-t）x+（3-t），
∴D的坐标为（0，3-t），
∴PK=OD=3-t，
∴E[t-1，（t-1）（3-t）+（3-t）]，即E[t-1，t（3-t）]，
∵点E在直线y=-x+3上，
∴-（t-1）+3=t（3-t），
t=2，
∴P（2，3）；

（3）如图3，过G作GN⊥AP于N，
设OF=m，则OG=2m，
∴Q[-m，（1-m）（3+m）]，
∴FQ=（1-m）（3+m），FB=3+m，
∴tan∠QBF=$\frac{FQ}{FB}$=1-m，
由（2）可知：直线AP的解析式为：y=x+1，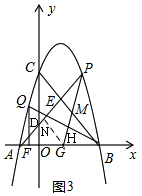
∴D（0，1），
∴OA=OD=1，
∴∠PAB=45°，
∵∠QHG=∠GBH+∠HGB=∠GBH+∠PAB+∠APG，
∵∠QHG-2∠GBH=45°，
∴∠GBH+45°+∠APG-2∠GBH=45°，
∴∠APG=∠GBH，
∴tan∠APG=tan∠QBF=1-m，
∵AN=GN=AG•sin45°=$\frac{\sqrt{2}}{2}$（2m+1），
由P（2，3），OA=1，得AP=3$\sqrt{2}$，
∴PN=AP-AN=3$\sqrt{2}$-$\frac{\sqrt{2}}{2}$（2m+1）=$\frac{5\sqrt{2}}{2}$-$\sqrt{2}$m，
∴tan∠APG=$\frac{NG}{PN}$=$\frac{\frac{\sqrt{2}}{2}（2m+1）}{\frac{5\sqrt{2}}{2}-\sqrt{2}m}$=1-m，
∴m=$\frac{1}{2}$或4，
∵OF＜OA，
∴m=$\frac{1}{2}$，
∴Q（-$\frac{1}{2}$，$\frac{7}{4}$）．

点评 本题是二次函数的综合题，考查了利用交点式求抛物线与x轴的交点及待定系数法、三角函数、三角形全等的性质和判定，本题利用了函数的解析式表示点的坐标，再由点的坐标表示线段的长，注意图形与坐标特点，第三问有难度，巧用已知∠QHG-2∠GBH=45°是关键．