练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在x轴上的点P的右侧有一点D，过点D作X轴的垂线交双曲线数学公式于点B，连接BO交AP于C，AP⊥x轴，设△AOC的面积为S1，梯形BCPD的面积为S2，则S1、S2的大小关系是


    1. A.
      S1＞S2
    2. B.
      S1＜S2
    3. C.
      S1=S2
    4. D.
      不确定
    C
    分析：根据A，B是反比例函数图象上的点，利用反比例函数图象上点的特征得出S△AOP=S△OBD，进而得出S1、S2的大小关系．
    解答：由题意可得出：S△AOP=S△OBD，
    ∵S△AOP-S△OCP=S△OBD-S△OCP，
    ∴△AOC的面积为S1，梯形BCPD的面积为S2，即S1=S2．
    故选：C．
    点评：此题主要考查了反比例函数y=中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=|k|．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    34、点A在x轴上，位于原点的右侧，距离坐标原点5个单位长度，则此点的坐标为
    （5，0）
    ；点B在y轴上，位于原点的下方，距离坐标原点5个单位长度，则此点的坐标为
    （0，-5）
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

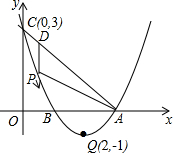    （2013•黔东南州一模）如图，已知抛物线y=ax2+bx+c（a≠0）的顶点坐标为Q（2，-1），且与y轴交于点C（0，3），与x轴交于A，B两点（点A在点B的右侧），点P是该抛物线上的一动点，从点C沿抛物线向点A运动（点P与A不重合），过点P作PD∥y轴，交AC于点D．
    （1）求该抛物线的函数关系式；
    （2）是否存在点P，使△ADP是直角三角形时？若存在，求点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

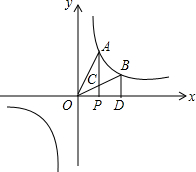    在x轴上的点P的右侧有一点D，过点D作X轴的垂线交双曲线y=
    1
    x
    于点B，连接BO交AP于C，AP⊥x轴，设△AOC的面积为S1，梯形BCPD的面积为S2，则S1、S2的大小关系是（　　）

    查看答案和解析>>

    科目：初中数学 来源：2012届浙江省椒江区九年级二模数学试卷（带解析） 题型：解答题

    如图①，在平面直角坐标系中，等腰直角△AOB的斜边OB在x轴上，顶点A的坐标为(3，3)，AD为斜边上的高．抛物线y＝ax2＋2x与直线y＝x交于点O、C，点C的横坐标为6．点P在x轴的正半轴上，过点P作PE∥y轴，交射线OA于点E．设点P的横坐标为m，以A、B、D、E为顶点的四边形的面积为S．
    【小题1】求OA所在直线的解析式．
    【小题2】求a的值．
    【小题3】当m≠3时，求S与m的函数关系式
    【小题4】如图②，设直线PE交射线OC于点R，交抛物线于点Q．以RQ为一边，在RQ的右侧作矩形RQMN，其中RN＝．直接写出矩形RQMN与△AOB重叠部分为轴对称图形时m的取值范围．

    查看答案和解析>>

    同步练习册答案