练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．先化简，再求值：（1-$\frac{x}{x-1}$）÷$\frac{1}{{x}^{2}-x}$，其中x=2．

    分析 根据运算顺序，先算括号里面的，再将除法转化为乘法计算可得．

    解答 解：原式=-$\frac{1}{x-1}$•x（x-1）
    =-x，
    当x=2时，原式=-2．

    点评 本题考查了分式的化简求值，掌握分式的通分和约分是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

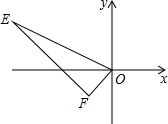    5．如图，点E（-4，2），F（-1，-1），以点O为位似中心，在点O的另一侧，按比例尺1：2，把△EFO缩小，则点E的对应点E′的坐标为（2，-1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

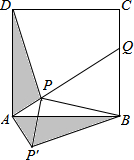    6．如图，点P是正方形ABCD内一点，点P到点A、B和D的距离分别为1，2$\sqrt{2}$，$\sqrt{10}$，△ADP沿点A旋转至△ABP′，连结PP′，并延长AP与BC相交于点Q．
    （1）求证：△APP′是等腰直角三角形；
    （2）判断△BPP′的形状，并求∠BPQ的度数；
    （3）求正方形ABCD的边AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知：x为实数，[x]表示不超过x的最大整数，如[3.14]=3，[1]=1，[-1.2]=-2．请你在学习，理解上述定义的基础上，解决下列问题：设函数y=x-[x]．
    （1）当x=2.15时，求y=x-[x]的值；
    （2）当0＜x＜2，求函数y=x-[x]的表达式，并画出函数图象；
    （3）在（2）的条件下，平面直角坐标系xOy中，以O为圆心，r为半径作圆，且r≤2，该圆与函数y=x-[x]恰有一个公共点，请直接写出r的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．对于两个不相等的实数a、b，我们规定符号max{a，b}表示a、b中较大的数，如：max{2，4}=4．按照这个规定．方程max{x，-x}=$\frac{2x+1}{x}$的解为（　　）
    A．$1-\sqrt{2}$B．$2-\sqrt{2}$C．$1-\sqrt{2}$或$1+\sqrt{2}$D．$1+\sqrt{2}$或-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．如图所示，AB∥CD，∠BEF和∠DFE的角平分线交于点G，∠1=100°，则∠2的度数是（　　）
    A．15°B．20C．30°D．40

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．济宁市某经济开发区，今年一月份工业产值达10亿元，第一季度总产值为75亿元，二、三月平均每月增长率是多少，若设平均每月的增长率为x，根据题意，可列方程为（　　）
    A．10（1+x）2=75B．10+10（1+x）+10（1+x）2=75
    C．10（1+x）+10（1+x）2=75D．10+10（1+x）2=75

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．如图，在?ABCD中，∠ABC，∠BCD的平分线BE，CF分别与AD相交于点E、F，BE与CF相交于点G，若AB=3，BC=5，CF=2，则BE的长为（　　）
    A．2$\sqrt{2}$B．4C．4$\sqrt{2}$D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．在一条公路上依次有A、B、C三个车站，甲、乙两车同时分别从A、B车站出发，匀速开往C车站，最终到达C车站，设甲、乙两车行驶x（h）后，与B车站的距离分别为y1、y2（km），y1、y2与x的函数关系如图所示．
    （1）A、C两车站间的距离为160km，图中的a=2；
    （2）求图中点P的坐标，并解释该点坐标所表示的实际意义；
    （3）若两车的距离不超过8km时能够利用车载对讲机联系，求甲、乙两车可以利用车载对讲机联系时x的取值范围．

    查看答案和解析>>

    同步练习册答案