
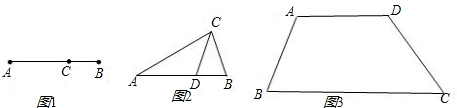
如图1,点C将线段AB分成两部分,如果 ,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果
,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果 ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
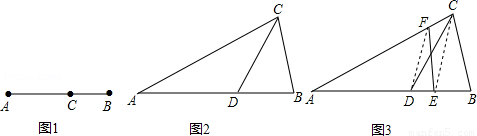
(1)研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点(如图2),则直线CD是△ABC的黄金分割线.你认为对吗?为什么?
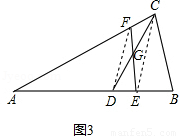
(2)研究小组在进一步探究中发现:过点C任作一条直线交AB于点E,再过点D作直线DF∥CE,交AC于点F,连接EF(如图3),则直线EF也是△ABC的黄金分割线.请你说明理由.
(1)对,理由见解析 (2)见解析
【解析】
试题分析:(1)设△ABC的边AB上的高为h,由三角形的面积公式即可得出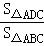 =
=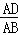 ,
,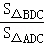 =
=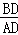 ,再由点D为边AB的黄金分割点可得出
,再由点D为边AB的黄金分割点可得出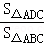 =
=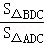 ,故可得出结论;
,故可得出结论;
(2)由DF∥CE可知△DEC和△FCE的公共边CE上的高也相等,故S△DEC=S△FCE,设直线EF与CD交于点G,由同底等高的三角形的面积相等可知S△DEG=S△FEG,故可得出S△ADC=S四边形AFGD+S△FCG=S△AEF,再由S△BDC=S四边形BEFC,再由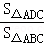 =
=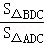 可知
可知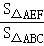 =
=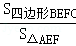 ,故直线EF也是△ABC的黄金分割线.
,故直线EF也是△ABC的黄金分割线.
解:(1)直线CD是△ABC的黄金分割线.理由如下:
设△ABC的边AB上的高为h.
∵S△ADC=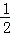 AD?h,S△EDC=
AD?h,S△EDC=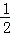 BD?h,S△ABC=
BD?h,S△ABC=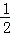 AB?h,
AB?h,
∴ =
=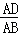 ,
,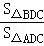 =
=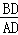 ,
,
又∵点D为边AB的黄金分割点,
∴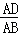 =
=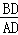 ,
,
∴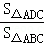 =
=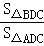 ,
,
∴直线CD是△ABC的黄金分割线;
(2)∵DF∥CE,
∴△DEC和△FCE的公共边CE上的高也相等,
∴S△DEC=S△FCE,
设直线EF与CD交于点G,
∴S△DEG=S△FCG,
∴S△ADC=S四边形AFGD+S△FCG=S四边形AFGD+S△DGE=S△AEF,
S△BDC=S四边形BEFC,.
又∵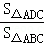 =
=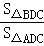 ,
,
∴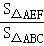 =
=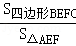 ,
,
∴直线EF也是△ABC的黄金分割线.
考点:相似形综合题;黄金分割.
点评:本题考查的是相似形综合题,涉及到平行线的性质及三角形的面积公式,根据题意理解黄金分割点及分割线的定义是解答此题的关键.


科目:初中数学 来源: 题型:
| AC |
| AB |
| BC |
| AC |
| S1 |
| S |
| S2 |
| S1 |
 1、V2的两个图形,且
1、V2的两个图形,且| V1 |
| V |
| V2 |
| V1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| AC |
| AB |
| BC |
| AC |
| S1 |
| S |
| S2 |
| S1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| AC |
| AB |
| BC |
| AC |
| S1 |
| S |
| S2 |
| S1 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| AC |
| AB |
| BC |
| AC |
| S1 |
| S |
| S2 |
| S1 |

查看答案和解析>>
科目:初中数学 来源: 题型:
(本小题满分10分)如图1,点C将线段AB分成两部分,如果AB : AC=AC : BC,那么称点C为线段![]() 的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线
的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线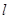 将一个面积为S的图形分成两部分,这两部分的面积分别为S1: S2,如果S : S1= S1: S2,,那么称直线
将一个面积为S的图形分成两部分,这两部分的面积分别为S1: S2,如果S : S1= S1: S2,,那么称直线![]() 为该图形的黄金分割线.
为该图形的黄金分割线.
(1)研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点(如图2),则直线CD是△ABC的黄金分割线.你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组探究发现:在(1)中,过点C任作AE交AB于E,再过点D作 ,交 AC于点F,连接EF(如图3),则直线EF是△ABC的黄金分割线.请说明理由.
,交 AC于点F,连接EF(如图3),则直线EF是△ABC的黄金分割线.请说明理由.
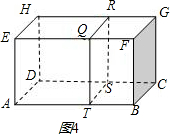
(4)如图4,点E是![]() ABCD的边AB的黄金分割点,过点E作
ABCD的边AB的黄金分割点,过点E作 ,交DC于点F,显然直线EF是
,交DC于点F,显然直线EF是![]() ABCD的黄金分割线.请你再画一条
ABCD的黄金分割线.请你再画一条![]() ABCD的黄金分割线,使它不经过
ABCD的黄金分割线,使它不经过![]() ABCD各边黄金分割点(保留必要的辅助线).
ABCD各边黄金分割点(保留必要的辅助线).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com