
 cm2,乙同学认为面积应该是
cm2,乙同学认为面积应该是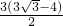 cm2而丙同学认为面积是
cm2而丙同学认为面积是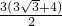 cm2等,你认为他们的说法全面吗?若你有不同结论,请你用你所学的数学知识求出其面积.
cm2等,你认为他们的说法全面吗?若你有不同结论,请你用你所学的数学知识求出其面积.
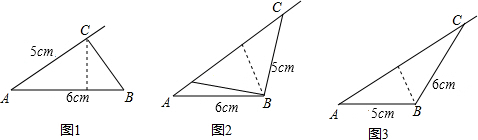
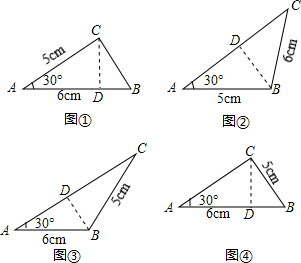 解:不全面,应该有四种情况.
解:不全面,应该有四种情况. AC=
AC= ,
, AB•CD=
AB•CD= ×6cm×
×6cm× cm=
cm= cm2;
cm2; AB=
AB= cm,AD=
cm,AD=
 cm;
cm;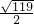 cm(勾股定理),
cm(勾股定理), AC•BD=
AC•BD= ×(
×(
 +
+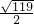 )×
)× cm=
cm=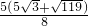 cm2;
cm2; AB=3cm,AD=3
AB=3cm,AD=3 cm;
cm; AC•BD=
AC•BD= ×(3
×(3 +4)×3cm=
+4)×3cm=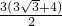 cm2;
cm2; xcm;
xcm;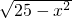 cm,
cm, x+
x+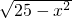 =6,
=6,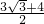 ,或x=
,或x=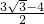 ,
, AB•CD=
AB•CD= ×(
×(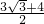 )×6cm=
)×6cm=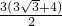 cm2;
cm2; AB•CD=
AB•CD= ×(
×(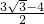 )×6cm=
)×6cm=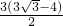 cm2;
cm2; cm2;
cm2;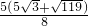 cm2;
cm2;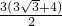 cm2;
cm2;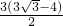 cm2.
cm2.

科目:初中数学 来源: 题型:
| 15 |
| 2 |
3(3
| ||
| 2 |
3(3
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年辽宁省本溪市九年级(上)第一次质量测试数学试卷(解析版) 题型:解答题
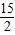 cm2,乙同学认为面积应该是
cm2,乙同学认为面积应该是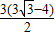 cm2而丙同学认为面积是
cm2而丙同学认为面积是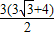 cm2等,你认为他们的说法全面吗?若你有不同结论,请你用你所学的数学知识求出其面积.
cm2等,你认为他们的说法全面吗?若你有不同结论,请你用你所学的数学知识求出其面积.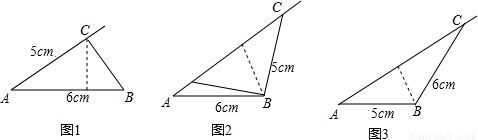
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com