分析:(1)根据等腰直角三角形的性质,知P1的横、纵坐标相等,再结合双曲线的解析式求得该点的坐标;
(2)主要是根据等腰直角三角形的性质和双曲线的解析式首先求得各个点的横坐标,再进一步求得其纵坐标,发现抵消的规律,从而求得代数式的值.
解答:解:(1)由△P
1OA
1是等腰直角三角形,得y
1=x
1,则有x
12=4,故x
1=±2(负舍),点P
1(2,2).
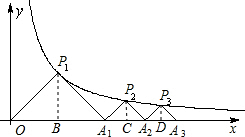
(2)解:过P
1作P
1B⊥OA
1于B,过P
2作P
2C⊥A
1A
2于C,
∵△OP
1A
1、△A
1P
1A
2是等腰直角三角形,
∴OB=BP
1=BA
1=x
1=y
1∴y
2=A
1C=OC-A
1B-OB=x
2-x
1-y
1,
同理可得:y
3=x
3-x
2-y
2,y
4=x
4-x
3-y
3,…,y
10=x
10-x
9-y
9,
又
yn=,则:
x2-4=,解得,x2=2+2.
∴
y2=2-2,
∴
x3-4=,x3=2+2,y3=2-2,
同理,依次得
x2=2+2,y2=2-2,
x3=2+2,y3=2-2,
x4=2+2,y4=2-2,
x5=2+2,y5=2-2,
…
x9=2+2,y9=2-2,
x
10=2
+2
,y
10=2
-2
,
∴y
1+y
2+y
3+…+y
10=
2+2-2+2-2+2-2+…+2-2+2-2=
2.
点评:此题主要是综合运用了等腰直角三角形的性质以及结合函数的解析式求得点的坐标.解答本题时同学们要找出其中的规律.

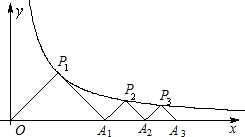 图象上,△P1OA1,△P2A1A2,△P3A2A3,…△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…An-1An都在x轴上
图象上,△P1OA1,△P2A1A2,△P3A2A3,…△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…An-1An都在x轴上


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案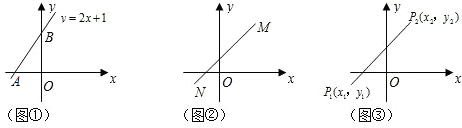
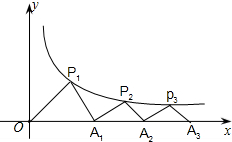 如图,P1(x1,y1),P2(x2,y2),在函数y=
如图,P1(x1,y1),P2(x2,y2),在函数y=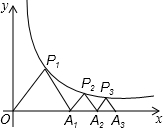 如图,P1(x1,y1),P2(x2,y2),Pn(xn,yn),…在函数 y=
如图,P1(x1,y1),P2(x2,y2),Pn(xn,yn),…在函数 y= 如图,P1(x1,y1),P2(x2,y2),…Pn(xn,yn)在函数y=
如图,P1(x1,y1),P2(x2,y2),…Pn(xn,yn)在函数y=