
���� ��1����A�ı��ΪxԪ����B�ı���ǣ�x-25��Ԫ������A��B��������ͬ���г���ʽ������⼴�ɣ�
��2�������A�ı����45Ԫ��B�ı����20Ԫʱ��A��B���������ٸ���A���������䣬B���ɶ���2m�������ܹ������з�����⼴�ɣ�
��� �⣺��1����A�ı��ΪxԪ����B�ı���ǣ�x-25��Ԫ����������ã�
$\frac{1800}{x}$=$\frac{800}{x-25}$��
��ã�x=45��
�����飬x=45��ԭ���̵Ľ⣬�ҷ������⣮
��x-25=45-25=20��Ԫ����
��A�ı����45Ԫ��B�ı����20Ԫ��
��2����A�ı����45Ԫ��B�ı����20Ԫʱ��A��B��������40����
��40��1-m%����45+20��1-m%����40+2m��=1800+800��
��ã�m1=0����ȥ����m2=35��
��m��ֵ��35��
���� ������Ҫ�����˷�ʽ���̵�Ӧ�ã��ؼ�����ȷ�������⣬�ҳ���Ŀ�еĵ�����ϵ���г����̣�ע��Ѳ�������Ľ���ȥ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{2}{3}$ | B�� | $\frac{2}{3}$ | C�� | -$\frac{3}{2}$ | D�� | $\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
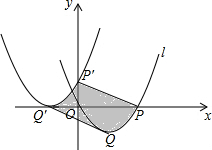 ��ͼ��������l��y=2x2-2x��������������������ƽ�ƣ�ʹ����Q�Ķ�Ӧ����Q�䣬������l��x����ҽ���P�Ķ�Ӧ����P�䣬��P�䡢Q�䶼���������ϣ��������ƽ�ƵĹ����У�������l�����߶�PQɨ�����������ͼ����Ӱ���ֵ������Ϊ$\frac{3}{4}$��
��ͼ��������l��y=2x2-2x��������������������ƽ�ƣ�ʹ����Q�Ķ�Ӧ����Q�䣬������l��x����ҽ���P�Ķ�Ӧ����P�䣬��P�䡢Q�䶼���������ϣ��������ƽ�ƵĹ����У�������l�����߶�PQɨ�����������ͼ����Ӱ���ֵ������Ϊ$\frac{3}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 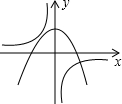 | B�� | 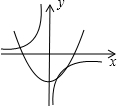 | C�� | 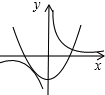 | D�� | 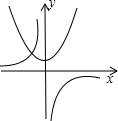 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
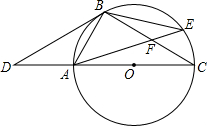 ��ͼ����D�ǡ�O��ֱ��CA�ӳ����ϵ�һ�㣬��B�ڡ�O�ϣ���AB=AD=AO��
��ͼ����D�ǡ�O��ֱ��CA�ӳ����ϵ�һ�㣬��B�ڡ�O�ϣ���AB=AD=AO���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
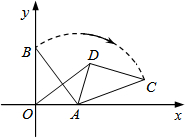 ��ƽ��ֱ������ϵ�У���֪��A��3��0����B��0��4��������BOA�Ƶ�A��˳ʱ�뷽����ת�á�CDA������OD������DOA=��OBAʱ��ֱ��CD�Ľ���ʽΪy=-$\frac{7}{24}$x+4��
��ƽ��ֱ������ϵ�У���֪��A��3��0����B��0��4��������BOA�Ƶ�A��˳ʱ�뷽����ת�á�CDA������OD������DOA=��OBAʱ��ֱ��CD�Ľ���ʽΪy=-$\frac{7}{24}$x+4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | ||
| C�� |  | D�� | 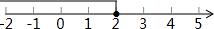 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com