75°
分析:由四边形ABCD为正方形,根据正方形的性质得到AB=AD,且∠DAB=90°,再由三角形MAB为等边三角形得到MA=AB,且∠MAB=60°,根据等量代换得到AD=AM,即三角形DAN为等腰三角形,由∠DAB-∠MAB求出∠DAN的度数,进而等腰三角形DAN的顶角度数,根据等腰三角形的两底角相等及内角和定理即可求出底角∠ADM的度数.
解答:∵四边形ABCD为正方形,
∴AB=AD,∠DAB=90°,
又△MAB是等边三角形,
∴AB=AM,∠MAB=60°,
∴AD=AM,∠DAM=∠DAB-∠MAB=90°-60°=30°,
∴∠ADM=
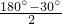
=75°.
故答案为:75°.
点评:此题考查了正方形的性质,等边三角形的性质,以及三角形的内角和定理.熟练掌握正方形及等边三角形的性质是解本题的关键.

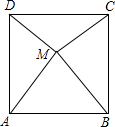 在正方形ABCD内取一点M,使△MAB是等边三角形,那么∠ADM的度数是________.
在正方形ABCD内取一点M,使△MAB是等边三角形,那么∠ADM的度数是________.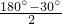 =75°.
=75°.
