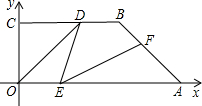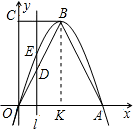
解:(1)过点B作BK⊥OA,
∵直角梯形OABC中,∠COA=90°,BC∥OA,OA=6,BC=3,AB=
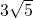
,
∴OK=BC=3,
∴AK=OA-OK=6-3=3,
在Rt∧ABK中:BK=
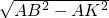
=6,
∴点B的坐标为(3,6),
∵抛物线过点O,
∴设抛物线的解析式为y=ax
2+bx,
∴
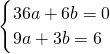
,
解得:
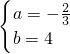
,
∴抛物线的解析式为:
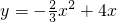
;
(2)设直线OB的解析式为:y=mx,
∴3m=6,
∴m=2,
∴直线OB的解析式为:y=2x;
设直线AB的解析式为:y=kx+b,
∴
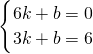
,
解得:
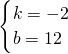
,
∴直线AB的解析式为:y=-2x+12,
当点D在OB上时,
DE=-

x
2+4x-2x=-

x
2+2x=-

(x-

)
2+

,
∴当t=

时,DE的最大值是

,
当点D在AB上时,
DE=-

x
2+4x+2x-12=-

x
2+6x-12=-

(x-

)
2+

,
∴当t=

时,DE的最大值是

,
∴t为

或

时,DE的最大值是

;
(3)存在:当D点在OB上时,以CD,BD,BC为对角线作出来图形,可得到三个菱形;当D点在OA上时,还可以得到一个菱形,得出:F
1(-


,6-


);F
2(

,9);F
3(

,

);F
4(


,6-


).
分析:(1)过点B作BK⊥OA,由直角梯形OABC中,∠COA=90°,BC∥OA,OA=6,BC=3,AB=
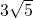
,即可求得点B的坐标,设抛物线的解析式为y=ax
2+bx,利用待定系数法即可求得抛物线的解析式;
(2)首先利用待定系数法求得直线OB与AB的解析式,再分别从当点D在OB上时与当点D在AB上时去分析,即可求得答案;
(3)由菱形的性质,分别从以CD,BD,BC为对角线去分析即可求得答案.
点评:此题考查了待定系数法求函数的解析式,考查了二次函数与一次函数的综合应用以及菱形的性质等知识.题目综合性很强,注意数形结合与方程思想的应用.

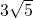 ,已知抛物线经过O、A、B
,已知抛物线经过O、A、B 三点.
三点.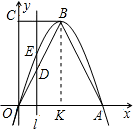 解:(1)过点B作BK⊥OA,
解:(1)过点B作BK⊥OA,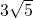 ,
,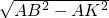 =6,
=6,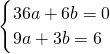 ,
,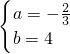 ,
,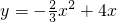 ;
;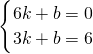 ,
,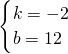 ,
, x2+4x-2x=-
x2+4x-2x=- x2+2x=-
x2+2x=- (x-
(x- )2+
)2+ ,
, 时,DE的最大值是
时,DE的最大值是 ,
, x2+4x+2x-12=-
x2+4x+2x-12=- x2+6x-12=-
x2+6x-12=- (x-
(x- )2+
)2+ ,
, 时,DE的最大值是
时,DE的最大值是 ,
, 或
或 时,DE的最大值是
时,DE的最大值是 ;
;
 ,6-
,6-
 );F2(
);F2( ,9);F3(
,9);F3( ,
, );F4(
);F4(
 ,6-
,6-
 ).
).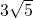 ,即可求得点B的坐标,设抛物线的解析式为y=ax2+bx,利用待定系数法即可求得抛物线的解析式;
,即可求得点B的坐标,设抛物线的解析式为y=ax2+bx,利用待定系数法即可求得抛物线的解析式;

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
 如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=
如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=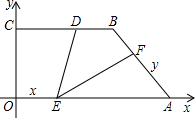 是BC上一点,BD=
是BC上一点,BD=