
分析 已知三角形两边的长和第三边的高,未明确这个三角形为钝角还是锐角三角形,所以需分情况讨论,即∠ABC是钝角还是锐角,然后利用勾股定理求解.
解答 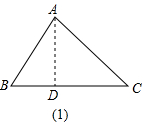 解:如图(1),△ABC中,AB=15,AC=20,BC边上高AD=12,
解:如图(1),△ABC中,AB=15,AC=20,BC边上高AD=12,
在Rt△ABD中AB=15,AD=12,
由勾股定理得,BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=9,
在Rt△ADC中AC=20,AD=12,
由勾股定理得,DC=$\sqrt{A{C}^{2}-A{D}^{2}}$=16,
则BC的长为BD+DC=9+16=25,
△ABC的周长为:15+20+25=60,
如图(2),同(1)的作法相同,BC=7,
△ABC的周长为:15+20+7=42,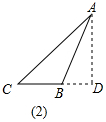 故答案为:42或60.
故答案为:42或60.
点评 本题主要考查了勾股定理,解决问题的关键是在直角三角形中用勾股定理求得线段的长.当已知条件中没有明确角的大小时,要注意讨论.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | 3$\sqrt{2}$-$\sqrt{2}$=3 | D. | $\frac{3}{\sqrt{3}}$=$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,六边形ABCDEF中,AB∥DE,BC∥EF,CD∥AF.现有以下结论:①∠A+∠C+∠E=360°;②∠B+∠C+∠D=360°;③AB=DE.其中正确的结论有( )
如图,六边形ABCDEF中,AB∥DE,BC∥EF,CD∥AF.现有以下结论:①∠A+∠C+∠E=360°;②∠B+∠C+∠D=360°;③AB=DE.其中正确的结论有( )| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
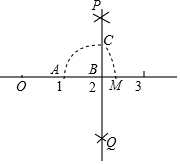 如图,数轴上点A、B对应的数分别是1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径作圆弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,当点M在点B的右侧时,点M对应的数是$\sqrt{5}$.
如图,数轴上点A、B对应的数分别是1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径作圆弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,当点M在点B的右侧时,点M对应的数是$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com