
 如图,CD是Rt△ABC斜边上的高,∠ACB=90°,BC=2,AB=3.
如图,CD是Rt△ABC斜边上的高,∠ACB=90°,BC=2,AB=3.分析 (1)证明△ACD∽△CBD,然后根据相似三角形的对应边的比相等即可证得;
(2)根据相似三角形的性质即可得到结论.
解答 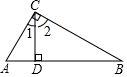 证明:∵Rt△ABC中,∠ACB=90°,
证明:∵Rt△ABC中,∠ACB=90°,
∴∠1+∠2=90°,
又∵CD是斜边AB上的高
∴∠ADC=∠CDB=90°,
∴∠1+∠A=90°,
∴∠A=∠2,
∴△ACD∽△CBD,
∴$\frac{AD}{CD}=\frac{CD}{BD}$,
∴CD2=AD•BD;
(2)∵∠ACB=90°,BC=2,AB=3,
∴AC=$\sqrt{5}$,
∴△ACD与△CBD的周长比=$\frac{AC}{BC}$=$\frac{\sqrt{5}}{2}$,△ACD与△CBD的面积比=($\frac{AC}{BC}$)2=$\frac{5}{4}$.
故答案为:$\frac{\sqrt{5}}{2}$,$\frac{5}{4}$.
点评 本题考查了相似三角形的判定与性质,证明等积式成立,常用的思路就是转化为证明比例式,从而转化为证明三角形相似.


科目:初中数学 来源: 题型:选择题
| A. | 图象的开口向下 | B. | 当x>1时,y随x的增大而减小 | ||
| C. | 当x<1时,y随x的增大而减小 | D. | 图象的对称轴是直线x=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$h | B. | 10h | C. | $\frac{80}{13}$ | D. | 以上答案都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
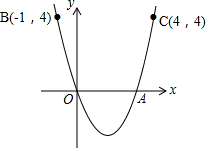 如图,抛物线y=ax2+bx经过原点O,与x轴的另一个交点是A点,点B(-1,4)和点C(4,4)是抛物线上的两个点,则点A的坐标为(3,0).
如图,抛物线y=ax2+bx经过原点O,与x轴的另一个交点是A点,点B(-1,4)和点C(4,4)是抛物线上的两个点,则点A的坐标为(3,0).查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省眉山市第九年级下学期第一次月考数学试卷(解析版) 题型:单选题
反比例函数 的图象,当
的图象,当 时,
时, 随
随 的增大而减小,则
的增大而减小,则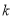 的取值范围是( )
的取值范围是( )
A.  B.
B.  C.
C. 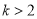 D.
D. 
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次月考数学试卷(解析版) 题型:判断题
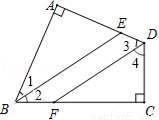
如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
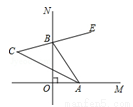
如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠NBA, BE的反向延长线与∠BAO的平分线交于点C,则∠C的度数是( )
A. 30° B. 45° C. 55° D. 60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com