练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

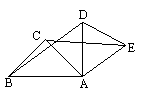
    如图所示，将等边△ABC绕点A旋转∠BAD的度数之后得到等边△ADE，连BD，CE．试问△BAD与△CAE能全等吗？请说明理由．

    答案：
    解析：

    　　答案：△BAD与△CAE是全等的．理由：因为△ABC为等边三角形，故AB＝BC＝AC．而△DAE是由△ABC绕点A旋转而成的，由旋转图形的性质可以知道：AD＝AB，AE＝AC，且∠BAD＝∠CAE，因而△BAD≌△CAE(SAS)．

    　　剖析：旋转、翻折、平移图形必是全等图形，故问题得以解决．


    提示：

    　　方法提炼：

    　　1．由旋转图形特征可知，∠BAD＝∠CAE，且AB＝AD，AC＝AE，又AB＝BC＝AC，从而可以利用SAS得到△BAD≌△CAE．

    　　2．旋转图形的性质是解答本题的关键．事实上，本题的条件可以弱一些，只需△ABC为等腰三角形，即AB＝AC即可．同学们不妨试试看．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图所示，在等边中△ABC，D、E分别是AB、AC上的点，DE∥BC，如图（1），然后将△ADE绕A点顺时针旋转120°，使B、A、E三点在同一直线上，得到图（2），M、N分别是BD、CE的中点，连接AM、AN、MN得到图（3），请解答下列问题：
    （1）在图（2）中，线段BD与线段CE的大小关系是
    BD=CE
    BD=CE
    ；
    （2）在图（3）中，△AMN与△ABC是相似三角形吗？请证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示 ，在等边中，D、E分别是AB、AC上的点，，如图（1），然后将绕A点顺时针旋转，使B、A、E三点在同一直线上，得到图（2），M、N分别是BD、CE的中点，连接AM、AN、MN得到图（3），请解答下列问题：

    （1）在图（2）中，线段BD与线段CE的大小关系是                         ；

    （2）在图（3）中，与是相似三角形吗？请证明你的结论。

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示 ，在等边中，D、E分别是AB、AC上的点，，如图（1），然后将绕A点顺时针旋转，使B、A、E三点在同一直线上，得到图（2），M、N分别是BD、CE的中点，连接AM、AN、MN得到图（3），请解答下列问题：
    （1）在图（2）中，线段BD与线段CE的大小关系是                         ；
    （2）在图（3）中，与是相似三角形吗？请证明你的结论。

    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：操作题

    如图所示，将等边三角形ABC，点A平移到B，再将平移后的图形绕点B顺时针旋转120°。

    查看答案和解析>>

    同步练习册答案