
 如图,AB和⊙O切于点B,AB=5,OB=3,则tanA=$\frac{3}{5}$.
如图,AB和⊙O切于点B,AB=5,OB=3,则tanA=$\frac{3}{5}$. 科目:初中数学 来源: 题型:填空题
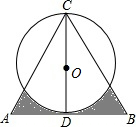 如图,△ABC是边长为4的等边三角形,D为AB边的中点,以CD为直径画圆,则图中阴影部分的面积为2.5$\sqrt{3}$-π(结果保留π).
如图,△ABC是边长为4的等边三角形,D为AB边的中点,以CD为直径画圆,则图中阴影部分的面积为2.5$\sqrt{3}$-π(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
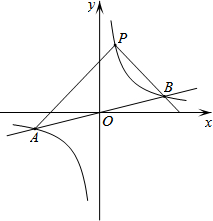 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 原料 型号 | 甲种原料(千克) | 乙种原料(千克) |
| A产品(每件) | 9 | 3 |
| B产品(每件) | 4 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 4月26日,2015黄河口(东营)国际马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是200$\sqrt{3}$+200米.
4月26日,2015黄河口(东营)国际马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是200$\sqrt{3}$+200米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )
如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )| A. | 由小到大 | B. | 由大到小 | ||
| C. | 不变 | D. | 先由小到大,后由大到小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com