
 (2013•内江)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:
(2013•内江)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:| 3 |
| 3 |
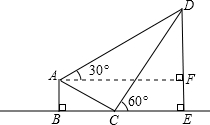 解:如图,过点A作AF⊥DE于F,
解:如图,过点A作AF⊥DE于F,| DE |
| tan60° |
| ||
| 3 |
| AB |
| BC |
| 1 | ||
|
| 3 |
| x-3 |
| tan30° |
| 3 |
| 3 |
| 3 |
| ||
| 3 |


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:
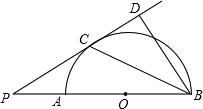 (2013•内江)如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC.
(2013•内江)如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•内江)如图,反比例函数y=
(2013•内江)如图,反比例函数y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•内江)如图,正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置,若正六边形的边长为2cm,则正六边形的中心O运动的路程为
(2013•内江)如图,正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置,若正六边形的边长为2cm,则正六边形的中心O运动的路程为查看答案和解析>>
科目:初中数学 来源: 题型:
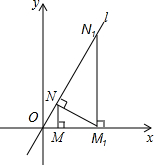 (2013•内江)如图,已知直线l:y=
(2013•内江)如图,已知直线l:y=| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com