
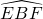 上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:AH•AQ是否为定值?若是,请求出这个定值;若不是,请说明理由.
上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:AH•AQ是否为定值?若是,请求出这个定值;若不是,请说明理由.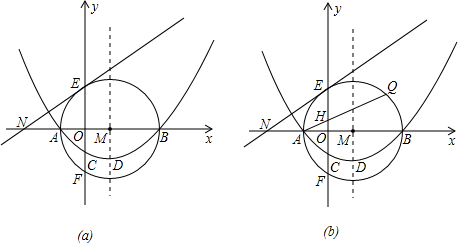
 =
= =
= =4.
=4.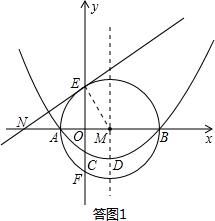
 .
. (x+2)(x-6)=
(x+2)(x-6)= x2-
x2- x-2.
x-2. x2-
x2- x-2=
x-2= (x-2)2-
(x-2)2- ,
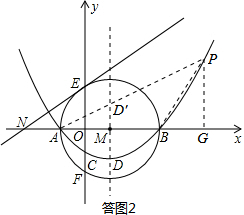
, ).
).
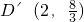 ,
,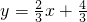 ,
,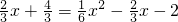 ,得x1=-2(舍去),x2=10.
,得x1=-2(舍去),x2=10.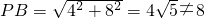
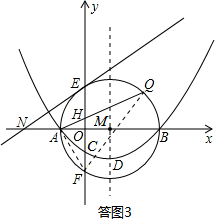
 ,∴AH•AQ=AF2…
,∴AH•AQ=AF2… )2=16(或利用AF2=AO•AB=2×8=16)
)2=16(或利用AF2=AO•AB=2×8=16)

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| ||
| 2 |
 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:

|
| t(秒) | 1 | 2 | 3 | … |
| x(米) | 20 | 40 | 60 | … |
| Y(米) | 5 | 20 | 45 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
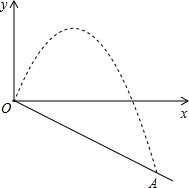 如图,东东站在斜坡OA上的O点处,向下抛出一块小石头,想看看自己能把小石头抛多远,已知他抛出小石头的运行路线可以用二次函数y=-
如图,东东站在斜坡OA上的O点处,向下抛出一块小石头,想看看自己能把小石头抛多远,已知他抛出小石头的运行路线可以用二次函数y=-| 9 |
| 16 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:101网校同步练习 初三数学 华东师大(新课标2001/3年初审) 华东师大版 题型:044
已知,如图,在平面直角坐标系xOy中,抛物线l1的解析式为y=-x2,将抛物线l1平移后得到抛线物l2,若抛物线l2经过点(0,2),且其顶点A的横坐标为最小正整数.

(1)求抛物线l2的解析式;
(2)说明将抛物线l1如何平移得到抛物线l2;
(3)若将抛物线l2沿其对称轴继续上下平移,得到抛物线l3,设抛物线l3的顶点为B,直线OB与抛物线l3的另一个交点为C.当OB=OC时,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源:河南省期中题 题型:解答题
 中,抛物线
中,抛物线 的解析式为
的解析式为 ,将抛物线
,将抛物线 平移后得到抛线物
平移后得到抛线物 ,若抛物线
,若抛物线 经过点(0,2),且其顶点A的横坐标为最小正整数。
经过点(0,2),且其顶点A的横坐标为最小正整数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com