在△ABC中.∠A=30°.∠B=45°.则△ABC是钝角三角形．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

5．在△ABC中，∠A=30°，∠B=45°，则△ABC是钝角三角形．

分析根据三角形内角和为180°，结合题意∠A=30°，∠B=45°，即可求出∠C的度数，进而判断△ABC的形状．

解答解：∵△ABC中，∠A=30°，∠B=45°，
∴∠C=180°-30°-45°=105°，
∴△ABC是钝角三角形，
故答案为：钝角．

点评本题主要考查了三角形内角和的知识，解答本题的关键是掌握三角形内角和为180°，此题难度不大．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

15．

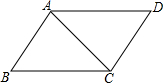我们知道平行四边形的一条对角线把这个平行四边形分成两个全等的三角形．如图，请你用“≌”表示这两个全等三角形，并写出图中相等的边和相等的角．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

16．

王师傅用4根木条钉成一个四边形木架，如图，要使这个木架不变形，他至少还要再钉上木条的条数为（　　）

A．

0根

B．

1根

C．

2根

D．

3根

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．设x₁，x₂是方程2x²+4x-3=0的两个根，利用根与系数的关系，求下列各式的值：
（1）（x₁+1）（x₂+1）；
（2）x₁²+x₂²；
（3）$\frac{x_2}{x_1}+\frac{x_1}{x_2}$；
（4）（x₁-x₂）²．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

20．某商户一周中各天的盈亏情况如下（盈余为正）：
128.5元，-27.6元，-13元，32元，-7元，38.3元，89元
一周总的盈亏情况如何？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

10．

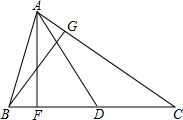如图，△ABC的边BC上的高为AF，中线为AD，AC边上的高为BG，已知AF=6，BC=10，BG=5．
（1）求△ABC的面积；
（2）求AC的长；
（3）说明△ABC和△ACD的面积关系．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

17．（1）为了探究三角形内角和，把∠B和∠A剪下后拼在一起，请你用量角器量一量，∠BCD=180°，所以∠A+∠B+∠ACB=180°．
（2）如图，延长BC至D，过点C作CE′∥AB
∵CE∥AB
∴∠1=∠B（两直线平行，同位角相等）
∠2=∠A（两直线平行，内错角相等）
∵∠1+∠2+∠ACB=180°（平角定义）
∴∠A+∠B+∠ACB=180°（等量代换）
归纳：三角形内角和等于180°．