
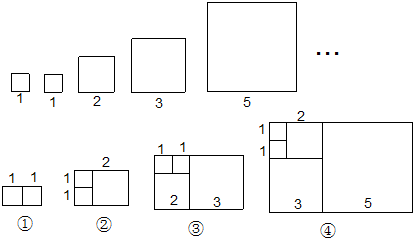
 彤彤将一些半径相同的小圆按如图所示的规律摆放,第①个图形由2个小圆构成,第②个图形由6个小圆构成,第③个图形由12个小圆构成,…,依此规律,当完成第⑧个图形时,一共所需要的小圆的个数是( )
彤彤将一些半径相同的小圆按如图所示的规律摆放,第①个图形由2个小圆构成,第②个图形由6个小圆构成,第③个图形由12个小圆构成,…,依此规律,当完成第⑧个图形时,一共所需要的小圆的个数是( )| A. | 72 | B. | 168 | C. | 230 | D. | 240 |
分析 由题意可知:第一个图形中有1×2=2个小圆,第二个图形中有2×3=6个小圆,第三个图形中有3×4=12个小圆,第四个图形中有4×5=20个小圆,…第n个图形有n(n+1)=(n2+n)个小圆,由此代入求得答案即可.
解答 解:第一个图形中有1×2=2个小圆,
第二个图形中有2×3=6个小圆,
第三个图形中有3×4=12个小圆,
第四个图形中有4×5=20个小圆,
…
第n个图形有n(n+1)=(n2+n)个小圆,
所以完成第⑧个图形时,一共所需要的小圆的个数是8×9=72.
故选:A.
点评 此题主要考查了图形的变化规律,通过归纳与总结结合图形得出图形个数之间的规律是解决问题的关键,注意公式必须符合所有的图形.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 序号 | ① | ② | ③ | ④ |
| 周长 | 6 | 10 | 16 | 26 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
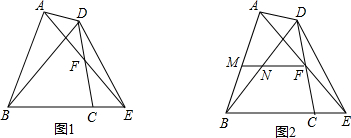
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
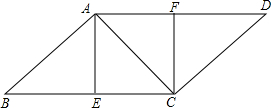 如图,在?ABCD中,OA=OC,E,F分别是边BC,AD的中点.
如图,在?ABCD中,OA=OC,E,F分别是边BC,AD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com