
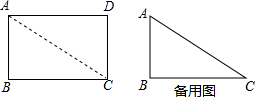
分析 (1)在Rt△ABC中,由∠B=90°,AB=2,BC=2$\sqrt{3}$,推出tan∠ACB=$\frac{AB}{BC}$=$\frac{\sqrt{3}}{3}$,推出∠ACB=30°,AC=2AB=4,由CA=CA′=4,∠ACA′=90°,推出AA′=$\sqrt{2}$AC.即可解决问题.
(2)分两种情形讨论①如图2中,当0<t≤2时,重叠部分是△CC′M,②如图3中,当2<t≤2$\sqrt{3}$时,重叠部分是四边形MNC′D′.分别计算即可.
解答 解:(1)如图1中,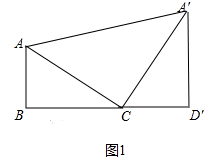
在Rt△ABC中,∵∠B=90°,AB=2,BC=2$\sqrt{3}$,
∴tan∠ACB=$\frac{AB}{BC}$=$\frac{\sqrt{3}}{3}$,
∴∠ACB=30°,AC=2AB=4,
∵CA=CA′=4,∠ACA′=90°,
∴AA′=4$\sqrt{2}$.
(2)①如图2中,当0<t≤2时,重叠部分是△CC′M,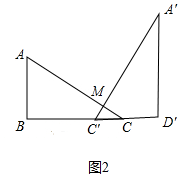
∵CC′=t,∠ACB=30°,∠A′C′D′=60°,
∴∠CMC′=90°,
∴C′M=$\frac{1}{2}$t,CM=$\frac{\sqrt{3}}{2}$t,
∴S=$\frac{1}{2}$•$\frac{1}{2}$t•$\frac{\sqrt{3}}{2}$t=$\frac{\sqrt{3}}{8}$t2,
②如图3中,当2<t<2$\sqrt{3}$时,重叠部分是四边形MNC′D′.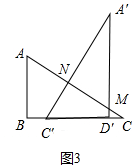
S=S△CNC′-S△CMD′=$\frac{\sqrt{3}}{8}$t2-$\frac{1}{2}$•(t-2)•$\frac{\sqrt{3}}{3}$•(t-2)=-$\frac{\sqrt{3}}{24}$t2+$\frac{2\sqrt{3}}{3}$t-$\frac{2\sqrt{3}}{3}$.
综上所述,S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{8}{t}^{2}}&{(0<t≤2)}\\{-\frac{\sqrt{3}}{24}{t}^{2}+\frac{2\sqrt{3}}{3}t-\frac{2\sqrt{3}}{3}}&{(2<t<2\sqrt{3})}\end{array}\right.$.
点评 本题可知作图-旋转变换、分段函数的应用,平移变换、勾股定理,直角三角形30度角性质等知识,解题的关键是灵活应用所学知解决问题,学会用分类讨论的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 调查某种计算机的使用寿命 | B. | 调查CCTV某档电视节目的收视情况 | ||
| C. | 调查我国七年级学生的视力情况 | D. | 调查你所在的班级学生的视力情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
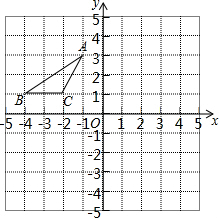 如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)(-2,1),先将△ABC向右平移5个单位,向上平移1个单位得△A1B1C1,再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2,点A1的对应点为点A2.
如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)(-2,1),先将△ABC向右平移5个单位,向上平移1个单位得△A1B1C1,再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2,点A1的对应点为点A2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A、D、B、E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.请你判断上面这个判断是否正确,如果正确,请给出说明;如果不正确,请添加一个适当条件使它成为正确的判断,并加以说明.
如图,已知点A、D、B、E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.请你判断上面这个判断是否正确,如果正确,请给出说明;如果不正确,请添加一个适当条件使它成为正确的判断,并加以说明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com