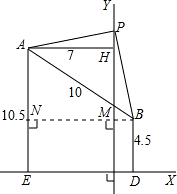
解:由笔直的高速公路X同侧,AB=10km,A,B到直线X的距离分别为AE=10.5km和BD=4.5km.知,BF=DF-BD=10.5-4.5=6,
∴AF=
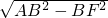
=
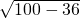
=8,
∵点B关于直线X的对称点是B
1,
∴BB
1⊥CD,∴BD=DB
1,
∴
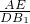
=
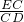
,
∴
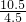
=
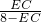
,
∴EC=5.6,
则CD=BD-EC=8-5.6=2.4,
AC=
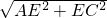
=
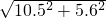
=11.9,
BC=
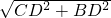
=
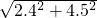
=5.1,
S
1=AC+BC=11.9+5.1=17km,
答:(1)S
1=17km;
(2)过B点作BN⊥AE,交公路Y于M,交AE于N,
∵Y⊥X,∴AN=HM=10.5-4.5=6,
∵ED=8(已求出),AH=7(已知),
∴BM=BN-NM=ED-AH=8-7=1,
设PH=x,则PM=HM+PH=6+x,
在Rt△AHP中,AP
2=AH
2+PH
2,
在Rt△PBM中,BP
2=PM
2+MB
2,
又∵AP=BP,
∴7
2+x
2=(x+6)
2+1
2,
解得x=1,则AP=
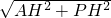
=
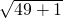
=5

,
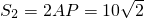
=14.14.
∵10

<17,
∴S
1>S
2.
分析:(1)先根据勾股定理求出BF的长,再利用点B关于直线X的对称点是B
1,求证△AEC∽△CDB
1,利用相似三角形对应变成比例求出EC和CD,然后利用勾股定理分别求出AC、BC即可.
(2)过B点作BN⊥AE,交公路Y于M,交AE于N,利用轴对称-最短线路问题求出BM,设PH=x,根据勾股定理和已知条件AP=BP列出方程,求出PH,然后即可求得AP,从而可以比较比较S
1,S
2的大小.
点评:此题主要考查学生对轴对称-最短线路问题和勾股定理的应用等知识点.步骤繁琐有一定的拔高难度,属于难题.

 )
)
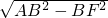 =
=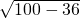 =8,
=8,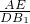 =
=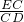 ,
,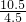 =
=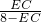 ,
,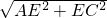 =
=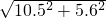 =11.9,
=11.9,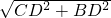 =
=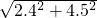 =5.1,
=5.1,
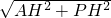 =
=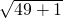 =5
=5 ,
,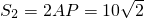 =14.14.
=14.14. <17,
<17,

 精英口算卡系列答案
精英口算卡系列答案