
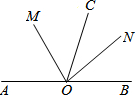
 已知:A、O、B在同一直线上,OC是任意一条射线,OM、ON分别为∠AOC、∠BOC的平分线,求∠MON的度数并说明理由.
已知:A、O、B在同一直线上,OC是任意一条射线,OM、ON分别为∠AOC、∠BOC的平分线,求∠MON的度数并说明理由. 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
 23、如图,A、B是一条河l同侧的两个村庄,且A、B两个村庄到河的距离分别是300m和500m,两村庄之间的距离AB为d(已知d2=400000m2),现要在河边l上建造一水厂,向A、B两村送水,铺设水管的工程费用为每米200元,修建该工程政府出资8万元,问两个村庄村民自筹资金至少多少元?
23、如图,A、B是一条河l同侧的两个村庄,且A、B两个村庄到河的距离分别是300m和500m,两村庄之间的距离AB为d(已知d2=400000m2),现要在河边l上建造一水厂,向A、B两村送水,铺设水管的工程费用为每米200元,修建该工程政府出资8万元,问两个村庄村民自筹资金至少多少元?查看答案和解析>>
科目:初中数学 来源: 题型:
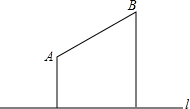 如图,A,B是笔直公路l同侧的两个村庄,且两个村庄到公路的距离分别是300m和500m,两村庄之间的距离为d(已知d2=400000m2),现要在公路上建一汽车停靠站,使两村到停靠站的距离之和最小,问最小值是多少?
如图,A,B是笔直公路l同侧的两个村庄,且两个村庄到公路的距离分别是300m和500m,两村庄之间的距离为d(已知d2=400000m2),现要在公路上建一汽车停靠站,使两村到停靠站的距离之和最小,问最小值是多少?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
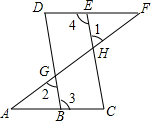 如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.
如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
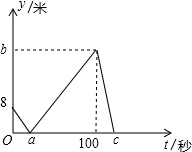 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,求a=
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,求a=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com