
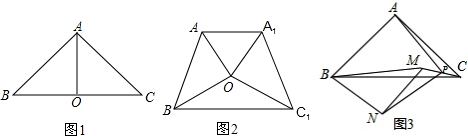
分析 (1)①过点O作MN⊥BC1于M,交AA1于N,只要证明ON⊥AA1即可解决问题;
②证△A1ON≌△OC1M,推出△A1ON和△OC1M的面积相等,同理可证△AON和△OBM的面积相等,即可得出答案;
③如图2中,作A1K⊥OA于K.因为${S}_{△AO{A}_{1}}$=$\frac{1}{2}$•OA•A1K,A1K≤OA1,所以当A1K=OA1时,即OA⊥OA1时,△AOA1的面积最大,此时△AOA1的面积=△AOB的面积,远程控制旋转角为90°,四边形AA1C1B的面积最大值为36.
(2)延长NP至E,使PE=NP,连接CE,AN,AE,证△PCE≌△PMN,推出CE=NM=BN,∠MNP=∠PEC,推出CE∥MN,C,设EC的延长线交BN的延长线于O,得出A、B、O、C四点共圆,推出∠ACE=∠ABN,证△ABN≌△ACE,推出AN=AE,∠ABN=∠EAC,求出∠EAN=90°,根据直角三角形斜边上中线等于斜边的一半推出即可.
解答 (1)①证明:如图2中,过点O作MN⊥BC1于M,交AA1于N,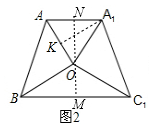
∵OB=OC1,
∴BM=C1M,∠BOM=∠C1OM,
∵∠AOB=∠A1OC1=90°,
∴∠AON+∠BOM=∠A1ON+∠C1OM=90°,
∴∠AON=∠A1ON,
∵AO=A1O,
∴ON⊥AA1,∵MN⊥BC1,
∴AA1∥BC1.
②证明:由①可知A1NO=90°=∠OMC1,
在△OMC1和△A1ON中
,$\left\{\begin{array}{l}{∠{A}_{1}NO=∠{C}_{1}MO}\\{∠N{A}_{1}O=∠{C}_{1}OM}\\{{A}_{1}O=O{C}_{1}}\end{array}\right.$,
∴△A1ON≌△OC1M(AAS),
∴△A1ON和△OC1M的面积相等,
同理可证△AON和△OBM的面积相等,
∴S△AOA1=S△BOC1.
③解:如图2中,作A1K⊥OA于K.
∵${S}_{△AO{A}_{1}}$=$\frac{1}{2}$•OA•A1K,
∴A1K≤OA1,
∴当A1K=OA1时,即OA⊥OA1时,△AOA1的面积最大,
此时△AOA1的面积=△AOB的面积,
∴旋转角为90°,四边形AA1C1B的面积最大值为36.
故答案为90°,36.
(2)证明:延长NP至E,使PE=NP,连接CE,AN,AE,设EC的延长线交BN的延长线于O.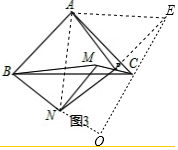
∵点P为MC的中点,
∴MP=CP,
∵在△PCE和△PMN中
$\left\{\begin{array}{l}{CP=PM}\\{∠EPC=∠MPN}\\{PE=NP}\end{array}\right.$,
∴△PCE≌△PMN(SAS),
∴CE=NM=BN,∠MNP=∠PEC,
∴CE∥MN,
∴∠BNM=∠BOC=90°,
又∵∠BAC=90°,
∴A、B、O、C四点共圆,
∴在四边形ABOC中,∠ACE=∠ABN,
∵在△ABN和△ACE中
$\left\{\begin{array}{l}{AB=AC}\\{∠ABN=∠ACE}\\{BN=CE}\end{array}\right.$,
∴△ABN≌△ACE(SAS),
∴AN=AE,∠ABN=∠EAC,
∵∠BAC=90°=∠BAN+∠NAC=∠EAC+∠NAC=∠EAN,
即∠EAN=90°,
∵点P为NE的中点,
∴PA=PN(直角三角形斜边上中线等于斜边的一半).
点评 本题考查了等腰三角形性质,全等三角形的性质和判定,直角三角形斜边上中线性质、四点共圆等知识点的应用,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
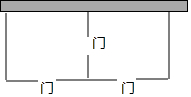 某农村拟建两间矩形饲养室,一面靠墙(墙足够长),中间用一道墙隔开,并在如图所示三处各留3m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为多少m2?
某农村拟建两间矩形饲养室,一面靠墙(墙足够长),中间用一道墙隔开,并在如图所示三处各留3m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为多少m2?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
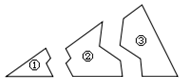 如图,小宇把一块三角形的玻璃打破成了三块,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是带( )去配.
如图,小宇把一块三角形的玻璃打破成了三块,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是带( )去配.| A. | 第①块 | B. | 第②块 | C. | 第③块 | D. | 第①和②块 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com