

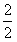 =1(s)
=1(s) 
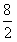 =4(s)
=4(s) 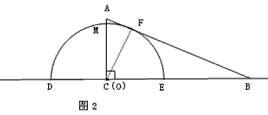
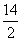 =7(s)
=7(s) 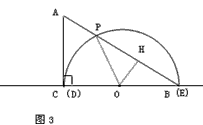
 =16(s)。
=16(s)。 
因为半圆O在运动中,它所在的圆与AC所在的直线相切只有上述①③两种情形,与AB所在的直线相切只有上述②④两种情形,与BC所在的直线始终相交,所以,只有t为1s,4s,7s,16s时,△ABC的一边所在的直线与半圆O所在的圆相切;
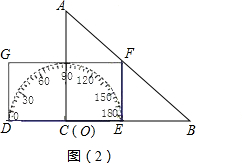
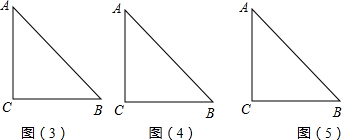
(2)当△ABC的一边所在的直线与半圆O所在的圆相切时,半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有如图2,与图3所示的两种情形。
①如图2,设OA与半圆O的交点为M,易知重叠部分是圆心角为90°,半径为6cm的扇形,所求重叠部分面积为:S扇形EOM=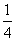
 ×62=9
×62=9 (cm2)
(cm2)
②如图3,设AB与半圆O的交点为P,连接OP,过点O作OH⊥AB,垂足为H,则点P到点H的距离PH=BH,在Rt△OBH中, ∠OBH=30。,OB=6cm,则OH=3cm,BH=3  cm,BP=6
cm,BP=6 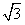 cm,
cm,
S△POB=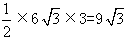 (cm2),又因为∠DOP=2∠DBP=60。,
(cm2),又因为∠DOP=2∠DBP=60。,
所以S扇形ODP=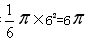 (cm2)。
(cm2)。
所求重叠部分面积为:S△POB + S扇形ODP =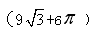 cm2
cm2


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
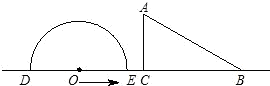
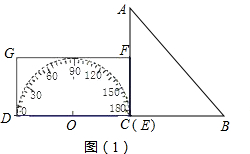
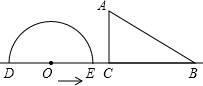 如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.当t为何值时,△ABC的一边所在直线与半圆O所在的圆相切?
如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.当t为何值时,△ABC的一边所在直线与半圆O所在的圆相切?查看答案和解析>>
科目:初中数学 来源:2005年初中毕业升学考试(江苏南京卷)数学(带解析) 题型:解答题
如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=
30°,BC=12cm.半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t (s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.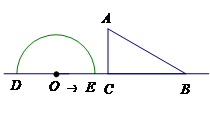
(1)当t为何值时,△ABC的一边所在的直线与半圆O所在的圆相切?
(2)当△ABC的一边所在的直线与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分,求重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源:2005年初中毕业升学考试(江苏南京卷)数学(解析版) 题型:解答题
如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=
30°,BC=12cm.半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t (s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
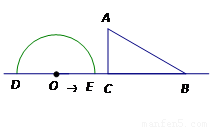
(1)当t为何值时,△ABC的一边所在的直线与半圆O所在的圆相切?
(2)当△ABC的一边所在的直线与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分,求重叠部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com